Под факторным анализом, понимается методика комплексного и системного изучения и измерения воздействия факторов на величину результативных показателей. 1 страница

Различают следующие типы факторного анализа:

- детерминированный и стохастический;

- прямой и обратный;

- одноступенчатый и многоступенчатый;

- статический и динамичный;

- ретроспективный и перспективный (прогнозный).

Детерминированный факторный анализ представляет собой методику исследования влияния факторов, связь которых с результативным показателем носит функциональный характер, т.е. когда результативный показатель представлен в виде произведения, частного или алгебраической суммы факторов.

Стохастический анализ представляет собой методику исследования факторов, связь которых с результативным показателем в отличие от функциональной является неполной, вероятностной (корреляционной). Если при функциональной (полной) зависимости с изменением аргумента всегда происходит соответствующее изменение функции, то при корреляционной связи изменение аргумента может дать несколько значений прироста функции в зависимости от Сочетания других факторов, определяющих данный показатель. Например, производительность труда при одном и том же уровне фондовооруженности может быть неодинаковой на разных предприятиях. Это зависит от оптимальности сочетания других факторов, воздействующих на этот показатель.

При прямом факторном анализе исследование ведется дедуктивным способом – от общего к частному. Обратный факторный анализ осуществляет исследование причинно-следственных связей способом логичной индукции – от частных, отдельных факторов к обобщающим.

Факторный анализ может быть одноступенчатым и многоступенчатым. Первый тип используется для исследования факторов только одного уровня (одной ступени) подчинения без их детализации на составные части. Например, у = а x b. При многоступенчатом факторном анализе проводится детализация факторов а и b на составные элементы с целью изучения их поведения. Детализация факторов может быть продолжена и дальше. В данном случае изучается влияние факторов различных уровней соподчиненности.

Необходимо различать также статический, применяемый при изучении влияния факторов на результативные показатели на соответствующую дату и динамический факторный анализ, представляющий собой методику исследования причинно-следственных связей в динамике.

И, наконец, факторный анализ может быть ретроспективным, который изучает причины прироста результативных показателей за прошлые периоды, и перспективным, который исследует поведение факторов и результативных показателей в перспективе.

Основные задачи факторного анализа представлены на рисунке 6.

Рисунок 6. Основные задачи факторного анализа

Отбор факторов для анализа того или другого показателя осуществляется на основе теоретических и практических знаний, приобретенных в этой отрасли. При этом обычно исходят из принципа: чем больший комплекс факторов исследуется, тем точнее будут результаты анализа. Вместе с тем необходимо иметь в виду, что если этот комплекс факторов рассматривается как механическая сумма, без учета их взаимодействия, без выделения главных, определяющих, то выводы могут быть ошибочными. В АХД взаимосвязанное исследование влияния факторов на величину результативных показателей достигается с помощью их систематизации, что является одним из основных методологических вопросов этой науки.

Важным методологическим вопросом в факторном анализе является определение формы зависимости между факторами и результативными показателями: функциональная она или стохастическая, прямая или обратная, прямолинейная или криволинейная. Здесь используется теоретический и практический опыт, а также способы сравнения параллельных и динамичных рядов, аналитических группировок исходной информации, графический и др.

Моделирование экономических показателей (детерминированное и стохастическое) также представляет собой сложную методологическую проблему в факторном анализе, решение которой требует специальных знаний и практических навыков в этой отрасли. В связи с этим этому вопросу в данном курсе уделяется много внимания.

Самый главный методологический аспект в экономическом анализе – расчет влияния факторов на величину результативных показателей, для чего в анализе используется целый арсенал способов, сущность, назначение, сфера применения которых и процедура расчетов рассматриваются в следующих главах.

И, наконец, последний этап факторного анализа – практическое использование факторной модели для подсчета резервов прироста результативного показателя, для планирования и прогнозирования его величины при изменении производственной ситуации.

Классификация факторов. Классификация факторов представляет собой распределение их по группам в зависимости от общих признаков. Она позволяет глубже разобраться в причинах изменения исследуемых явлений, точнее оценить место и роль каждого фактора в формировании величины результативных показателей.

Исследуемые в анализе факторы могут быть классифицированы по разным признакам (рисунке 7).

В экономическом анализе очень важное значение отводится измерению влияния каждого фактора на результаты хозяйственной деятельности, то их разделяют на количественные и качественные, сложные и простые, прямые и косвенные, измеримые и неизмеримые.

Количественными считаются факторы, которые выражают количественную определенность явлений (количество рабочих, оборудования, сырья и т.д.). Качественные факторы определяют внутренние качества, признаки и особенности изучаемых объектов (производительность труда, качество продукции, плодородие почвы и т.д.).

Большинство изучаемых факторов по своему составу являются сложными, состоят из нескольких элементов. Однако, есть и такие, которые не раскладываются на составные части. В связи с этим факторы делятся на сложные (комплексные) и простые (элементные). Примером сложного фактора является производительность труда, а простого - количество рабочих дней в отчетной периоде.

Как уже указывалось, одни факторы оказывают непосредственное влияние на результативный показатель, другие – косвенное. По уровню соподчиненности (иерархии) различают факторы первого, второго, третьего и последующих уровней подчинения. К факторам первого уровня относятся те, которые непосредственно влияют на результативный показатель. Факторы, которые определяют результативный показатель косвенно, при помощи факторов первого уровня, называются факторами второго уровня и т.д. На рисунке 7 показано, что факторами первого уровня являются среднегодовая численность рабочих и среднегодовая выработка продукции одним рабочим. Количество отработанных дней одним рабочим и среднедневная выработка - факторы второго уровня относительно валовой продукции. К факторам же третьего уровня относятся продолжительность рабочего дня и среднечасовая выработка.

Рисунок 7. Классификация факторов

Воздействие отдельных факторов на результативный показатель может быть определено количественно. Вместе с тем имеется целый ряд факторов, влияние которых на результаты деятельности предприятий не поддается непосредственному измерению, например, обеспеченность персонала жильем, детскими учреждениями, уровень подготовки кадров и др.

Систематизация факторов в анализе хозяйственной деятельности. Системный подход в АХД вызывает необходимость взаимосвязанного изучения факторов с учетом их внутренних и внешних связей, взаимодействия и соподчиненности, что достигается с помощью систематизации. Систематизация в целом – это размещение изучаемых явлений или объектов в определённом порядке с выявлением их взаимосвязи и подчиненности.

Одним из способов систематизации факторов является создание детерминированных факторных систем. Создать факторную систему – значит представить изучаемое явление в виде алгебраической суммы, частного или произведения нескольких факторов, определяющих его величину и находящихся с ним в функциональной зависимости.

Например, объем валовой продукции промышленного предприятия можно представить в виде произведения двух факторов первого порядка: среднего количества рабочих и среднегодовой выработки продукции одним рабочим за год, которая в свою очередь зависит непосредственно от количества отработанных дней одним рабочим в среднем за год и среднедневной выработки продукции рабочим. Последняя также может быть разложена на продолжительность рабочего дня и среднечасовую выработку (рисунок 8).

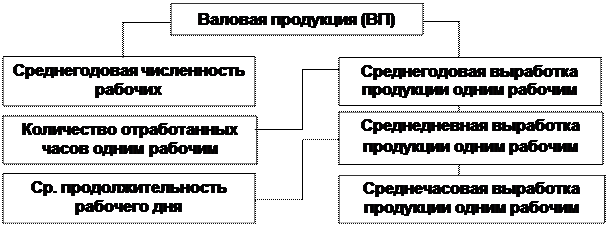Рисунок 8. Детерминированная факторная система валовой продукции

Развитие детерминированной факторной системы достигается, как правило; за счет детализации комплексных факторов. Элементные (в нашем примере – количество рабочих, количество отработанных дней, продолжительность рабочего дня) не раскладываются на сомножители, так как по своему содержанию они однородны. С развитием системы комплексные факторы постепенно детализируются на менее общие, те в свою очередь еще на менее общие, постепенно приближаясь по своему аналитическому содержанию к элементным (простым).

Большое значение в исследовании стохастических взаимен связей имеетструктурно-логический анализ связи между изучаемыми показателями. Он позволяет установить наличие или отсутствие причинно-следственных связей между исследуемыми показателями, изучить направление связи, форму зависимости и т.д., что очень важно при определении степе-1 ни их влияния на изучаемое явление и при обобщении результатов анализа.

Анализ структуры связи изучаемых показателей в экономическом анализе осуществляется с помощью построения структурно – логической блок-схемы, которая позволяет установить наличие и на” правление связи не только между изучаемыми факторами и результативным показателем, но и между самими факторами. Построив блок-схему, можно увидеть, что среди изучаемых факторов имеются такие, которые более или менее непосредственно воздействуют на результативный показатель, и такие, которые воздействуют не столько на результативный показатель, сколько друг на друга.

Исследование взаимосвязей между факторами показывает, что из всех изучаемых факторов отсутствует причинно-следственная связь между качеством семян, количеством удобрении и механизацией производства. Отсутствует также непосредственная обратная зависимость данных показателей от уровня урожайности культуры. Все остальные факторы прямо или косвенно влияют друг на друга.

Таким образом, систематизация факторов позволяет более глубоко изучить взаимосвязь факторов при формировании величины изучаемого показателя, что имеет очень важное значение на следующих этапах анализа, особенно на этапе моделирования исследуемых показателей.

Детерминированное моделирование и преобразование факторных систем. Одной из задач факторного анализа является моделирование взаимосвязей между результативными показателями и факторами, которые определяют их величину.

Моделирование – это один из важнейших методов научного познания, с помощью которого создается модель (условный образ) объекта исследования. Сущность его заключается в том, что взаимосвязь исследуемого показателя с факторными передается в форме конкретного математического уравнения.

В факторном анализе различают модели детерминированные (функциональные) и стохастические (корреляционные). С помощью детерминированных факторных моделей исследуется функциональная связь, между результативным показателем (функцией) и факторами (аргументами).

При моделировании детерминированных факторных систем необходимо выполнять ряд требований.

1. Факторы, включаемые в модель, и сами модели должны иметь определенно выраженный характер, реально существовать, а не быть придуманными абстрактными величинами или явлениями.

2. Факторы, которые входят в систему, должны быть не только необходимыми элементами формулы, но и находиться в причинно-следственной связи с изучаемыми показателями. Иначе говоря, построенная факторная система должна иметь познавательную ценность. Факторные модели, которые отражают причинно-следственные отношения между показателями, имеют значительно большее познавательное значение, чем модели, созданные при помощи приемов математической абстракции. Последнее можно проиллюстрировать следующим образом. Возьмем две модели:

1) ВП = ЧР * ГВ;

2) ГB = BП / ЧP,

где ВП – валовая продукция предприятия;

ЧР – численность работников на предприятии;

ГВ – среднегодовая выработка продукции одним работником.

В первой системе факторы находятся в причинной связи с результативным показателем, а во второй – в математическом соотношении. Значит, вторая модель, построенная на математических зависимостях, имеет меньшее познавательное значение, чем первая.

3. Все показатели факторной модели должны быть количественно измеримыми, т.е. должны иметь единицу измерения и необходимую информационную обеспеченность.

4. Факторная модель должна обеспечивать возможность измерения влияния отдельных факторов, это значит, что в ней должна учитываться соразмерность изменений результативного и факторных показателей, а сумма влияния отдельных факторов должна равняться общему приросту результативного показателя.

В детерминированном анализе выделяют следующие типы наиболее часто встречающихся факторных моделей.

Аддитивные модели:

Они используются в тех случаях, когда результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей.

Мультипликативные модели:

Этот тип моделей применяется тогда, когда результативный показатель представляет собой произведение нескольких факторов.

Кратные модели:

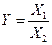
Они применяются тогда, когда результативный показатель получают делением одного факторного показателя на величину другого.

Смешанные (комбинированные) модели:

Это сочетание в различных комбинациях предыдущих моделей

Моделирование мультипликативных факторных систем в экономическом анализе осуществляется путем последовательного расчленения факторов исходной системы на факторы-сомножители. Например, при исследовании процесса формирования объема производства продукции (см. рисунок 8) можно применять такие детерминированные модели, как:

Эти модели отражают процесс детализации исходной факторной системы мультипликативного вида и расширения ее за счет расчленения на сомножители комплексных факторов. Степень детализации и расширения модели зависит от цели исследования, а также от возможностей детализации и формализации показателей в пределах установленных правил.

Аналогичным образом осуществляется моделирование аддитивных факторных систем за счет расчленения одного или нескольких факторных показателей на составные элементы.

К классукратных моделей применяют следующие способы их преобразования: удлинения, формального разложения, расширения и сокращения.

Первый метод предусматривает удлинение числителя исходной модели путем замены одного или нескольких факторов на сумму однородных показателей. Например, себестоимость единицы продукции можно представить в качестве функции двух факторов: изменения суммы затрат (3) и объема выпуска продукции (VBП). Исходная модель этой факторной системы будет иметь вид

Если общую сумму затрат (З) заменить отдельными их элементами, такими, как заработная плата (3П), сырье и материалы (СМ), амортизация основных средств (А), накладные расходы (HP) и др., то детерминированная факторная модель будет иметь вид аддитивной модели с новым набором факторов:

где X₁ – трудоемкость продукции;

Х₂ – материалоемкость продукции;

Х₃ – фондоемкость продукции;

Х₄ – уровень накладных расходов.

Способ формального разложения факторной системы предусматривает удлинение знаменателя исходной факторной модели путем замены одного или нескольких факторов на сумму или произведение однородных показателей. Если

В = L + М + N + Р, то

В результате получили конечную модель того же вида, что и исходной факторной системы (кратную модель). На практике такое разложение встречается довольно часто. Например, при анализе показателя рентабельности производства

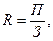
где П – сумма прибыли от реализации продукции;

З - сумма затрат на производство и реализацию продукции.

Если сумму затрат заменить на отдельные ее элементы, конечная модель в результате преобразования приобретет следующий вид:

Себестоимость, одного тонно-километра зависит от сумм затрат на содержание и эксплуатацию автомобиля (З) и от её среднегодовой выработки (ГВ). Исходная модель этой систем будет иметь вид: С_ткм = З/ГВ. Учитывая, что среднегодовая выработка машины в свою очередь зависит от количества отработанных дней одним автомобилем за год (Д), продолжительности смены (П) и среднечасовой выработки (ЧВ), и можем значительно удлинить эту модель и разложить прирост себестоимости на большее количество факторов:

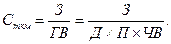
Метод расширения предусматривает расширение исходной факторной модели за счет умножения числителя и знаменателя дроби на один или несколько новых показателей. Например, если в исходную модель У = А/В ввести новый показатель с, то модель примет вид

В результате получилась конечная мультипликативная модель в виде произведения нового набора факторов.

Этот способ моделирования очень широко применяется в анализе. Например, среднегодовую выработку продукции одним работником (показатель производительности труда) можно записать таким образом: ГВ = ВП / ЧР. Если ввести такой показатель, как количество отработанных дней всеми работниками (D), то получим следующую модель годовой выработки:

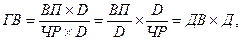
где ДВ – среднедневная выработка;

Д – количество отработанных дней одним работником.

После введения показателя количества отработанных часов всеми работниками (Т) получим модель с новым набором факторов: среднечасовой выработки (УД), количества отработанных дней одним работником (Д) и продолжительности рабочего дня (П):

Способ сокращения представляет собой создание новой факторной модели путем деления числителя и знаменателя дроби на один и тот же показатель:

В данном случае получается конечная модель того же типа, что и исходная, однако с другим набором факторов.

И снова практический пример. Как известно, экономическая рентабельность работы предприятия рассчитывается делением суммы прибыли (П) на среднегодовую стоимость основного оборотного капитала предприятия (KL).

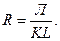
Если числитель и знаменатель разделим на объем реализации продукции (товарооборот), то получим кратную модель, но с новым набором факторов: рентабельности продаж и капиталоемкости продукции:

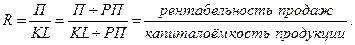
И еще один пример. Фондоотдача (ФО) определяется отношением валовой (ВП) или товарной продукции (ТП) к среднегодовой стоимости основных производственных фондов (ОПФ):

Разделив числитель и знаменатель на среднегодовое количество рабочих (ЧР), получим более содержательную кратную модель с другими факторными показателями: среднегодовой выработки продукции одним рабочим (ГВ), характеризующей уровень производительности труда, и фондовооруженности труда (Фв):

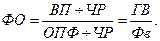
Необходимо заметить, что на практике для преобразований одной и той же модели может быть последовательно использовано несколько методов. Например:

где ФО – фондоотдача;

РП – объем реализованной продукций (выручка);

C – себестоимость реализованной продукции;

П – прибыль;

ОПФ – среднегодовая стоимость основных производственных фондов;

ОС – средние остатки оборотных средств

В этом случае для преобразования исходной факторной модели, которая построена на математических зависимостях, использованы способы удлинения и расширения. В результате получилась более содержательная модель, Которая имеет большую познавательную ценность, так как учитывает причинно-следственные связи между показателями. Полученная, конечная модель позволяет исследовать, как влияют на фондоотдачу рентабельность основных средств производства, соотношения между основными и оборотными средствами, а также коэффициент оборачиваемости оборотных средств.

Таким образом, результативные показатели могут быть разложены на составные элементы (факторы) различными способами и представлены в виде различных типов детерминированных моделей. Выбор способа моделирования зависит от объекта исследования, поставленной цели, а также от профессиональных знаний и навыков исследователя.

Процесс моделирования факторных систем – очень сложный и ответственный момент в экономическом анализе. От того, насколько реально и точно созданные модели отражают связь между исследуемыми показателями, зависят конечные результаты анализа.

Способы количественной оценки изменений факторов и их влияния на результат. Способ цепной подстановки Способ цепной подстановки. Из множества способов количественной оценки влияния факторов на изменение экономических показателей использующихся в экономическом анализе можно выделить наиболее используемые. Вот некоторые из них:

- способ цепной подстановки

- индексный способ

- способ абсолютных разниц

- способ относительных разниц

- способ пропорционального деления

- интегральный способ

- логарифмирования и др.

Одним из важнейших методологических вопросов в экономическом анализе является определение величины влияния отдельных факторов на прирост результативных показателей. В детерминированном факторном анализе (ДФА) для этого используются следующие способы:цепной подстановки, индексный, абсолютных разниц, относительных разниц, пропорционального деления, интегральный, логарифмирования и др.

Первых четыре способа основываются на методе элиминирования. Элиминировать – значит устранить, отклонить, исключить воздействие всех факторов на величину результативного показателя, кроме одного. Этот метод исходит из того, что все факторы изменяются независимо друг от друга: сначала изменяется один, а все другие остаются без изменения, потом изменяются два, затем три и т.д., при неизменности остальных. Это позволяет определить влияние каждого фактора на величину исследуемого показателя в отдельности.

Типы детерминированных моделей, в которых применяется способ цепной подстановки. Наиболее универсальным из них является способ цепной подстановки. Он используется для расчета влияния факторов во всех типах детерминированных факторных моделей: аддитивных, мультипликативных, кратных и смешанных (комбинированных). Этот способ позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого факторного показателя в объеме результативного показателя на фактическую в отчетном периоде. С этой целью определяют ряд условных величин результативного показателя, которые учитывают изменение одного, затем двух, трех и т.д. факторов, допуская, что остальные не меняются. Сравнение величины результативного показателя до и после изменения уровня того или другого фактора позволяет элиминироваться от влияния всех факторов, кроме одного, и определить воздействие последнего на прирост результативного показателя.

Рассмотрим пример расчета влияния факторов на прирост результативного показателя в мультипликативных моделях. Порядок применения этого способа рассмотрим на следующем примере (таблица 1).

Как нам уже известно, объем валовой продукции (ВП) зависит от двух основных факторов первого уровня: численности рабочих (ЧР) и среднегодовой выработки (ГВ). Имеем двухфакторную мультипликативную модель: ВП = ЧР * ГВ.

Алгоритм расчета способом цепной подстановки для этой модели:

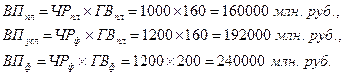
Как видим, второй показатель валовой продукции отличается от первого тем, что при его расчете принята фактическая численность рабочих вместо запланированной. Среднегодовая выработка продукции одним рабочим в том и другом случае плановая. Значит, за счет увеличения количества рабочих выпуск продукции увеличился на 32000 млн. руб. (192000 – 160000).

Третий показатель отличается от второго тем, что при расчете его величины выработка рабочих принята по фактическому уровню вместо плановой. Количество же работников в обоих случаях фактическое. Отсюда за счет повышения производительности труда объем валовой продукции увеличился на 48 000 млн. руб. (240000 – 192000).

Таблица 1.
Данные для факторного анализа объема валовой продукции

Показатель	Усл. обозначение	План	Факт	+,-	Выполнение плана, %
Валовая продукция, млн. руб.	ВП			+80000
Среднегодовая численность рабочих, чел.	ЧР			+200
Отработано всеми рабочими за год:
дней	D			+57200	122,88
часов	T			+334720	116,736
Среднегодовая выработка одного рабочего, млн. руб.	ГВ			+40
Количество отработанных дней одним рабочим за год	Д			+6	102,4
Среднедневная выработка продукции одним рабочим, тыс. руб.	ДВ		781,25	+141,25	122,1
Средняя продолжительность рабочего дня, ч	П		7,6	-0,4
Среднечасовая выработка, тыс. руб.	ЧВ		102,796	+22,796	128,5

Таким образом, перевыполнение плана по объему валовой продукции явилось результатом влияния следующих факторов:

а) увеличения численности рабочих: +32 000 млн. руб.

б) повышения уровня производительности труда: +48 000 млн. руб.

Итого: +80000 млн. руб.

Дата добавления: 2017-02-01