
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Идея алгоритма Фаулкса
|
|
|
|
Итак, попытаемся найти путь в этом лабиринте, устанавливая возможные иерархии между различными частями одежды.
Для простоты записи мы обозначим их буквами:
А — брюки, В— жилет, С — пиджак, D — галстук, Е— пальто, F — носки, G — обувь, H — перчатки.
Мы уверены, что наш друг при всей своей ловкости не сможет, например, надеть жилет позже пиджака; мы выразим это необходимое условие обозначением
В <С
(что можно читать как « Впредшествует C»). Зато ему безразлично, надеть ли прежде жилет или галстук, что запишется в виде 
В >< D.
Наконец, мы считаем почти немыслимым, чтобы он не обулся немедленно после того, как надел носки; отсюда напрашиваются общие обозначения
F |<G
( Fнепосредственно предшествует G).
Подытожим подобные соотношения различных типов, допускаемые нашей задачей:
А < В, D, С; В < С; В >< D, F;
С < Е;D < С, Е, H; F |<G; G < С, H.
Эти соотношения могут выражаться рисунком или графом, о чем мы уже неоднократно говорили.
Граф, сам по себе, может быть представлен матрицей, если условиться обозначать единицей все реализуемые связи буквы, стоящей в строке, с буквой, указывающей столбец.
Матрица 1
| A | B | C | D | E | F | G | H | |
| A | ||||||||
| B | ||||||||
| C | ||||||||
| D | ||||||||
| E | ||||||||
| F | ||||||||
| G | ||||||||
| H |

Рис. 16.1.
Теперь мы хотим определить, существует ли такой путь между какой-нибудь буквой, служащей входом, и какой-нибудь буквой, служащей выходом, который дал бы возможность нашему другу Фреголи одеться, не нарушая выписанных выше соотношений.
Чтобы справиться с этой задачей, выполним довольно специфическую операцию — умножение матрицы М(матрицы 1) на себя, заменяя, однако, обычную арифметическую сумму булевой суммой элементов.
Мы не будем останавливаться на обсуждениях по поводу булевой суммы, таблицу которой мы приводим ниже и которая была предметом специального исследования в гл. 11:
| + | A | B | A + B |
Таким образом, член произведения, расположенный в третьей клетке первой строки, является произведением строки A на столбец C и равен 1, если рассматривать булеву сумму элементов
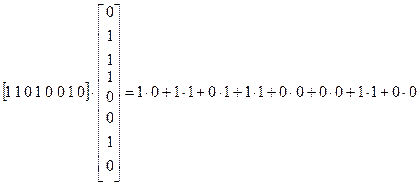
Мы видим, что полученная матрица, которую мы обозначим
через М[2], будет содержать только нули и единицы. Так же будет обстоять дело и с М[4].
| М[2]= | A | B | C | D | E | F | G | H | |
| A | (1) | (1) | (1) | ||||||
| B | (1) | (1) | |||||||
| C | (1) | ||||||||
| D | (1) | (1) | |||||||
| E | |||||||||
| F | (1) | (1) | (1) | ||||||
| G | (1) | ||||||||
| H |
Единицы, обозначенные (1), не входили в М и составляют часть М[2].
| М[4]= | A | B | C | D | E | F | G | H | |
| A |  1 1
|

| |||||||
| B | |||||||||
| C | |||||||||
| D |  1 1
|  1 1
| |||||||
| E | |||||||||
| F |  1 1
| ||||||||
| G | |||||||||
| H |
Из матрицы М[4] видно, что A является элементом, за которым может следовать (прямо или косвенно) любой другой, но которому никакой элемент не может предшествовать.
| М′[8]= | B | C | D | E | F | G | H | |
| B | ||||||||
| C | ||||||||
| D | ||||||||
| E | ||||||||
| F | ||||||||
| G | ||||||||
| H |
Для вычисления М[8] нет надобности сохранять столбец и строку Aв М[4]; мы получаем М′[8], относительно которой легко заметить, что она в точности равна соответствующей части М[4].
В этих условиях мы должны, согласно алгоритму Фаулкса[1], прекратить наши операции. Перестановкой строк и столбцов матрицу М[4] можно представить в форме М[4]; это означает, что задача порождает пять упорядоченных подграфов.
| М[4]= | A | F | B | D | G | C | E | H | |
| A | |||||||||
| F | |||||||||
| G | |||||||||
| E | |||||||||
| H | |||||||||
| D | |||||||||
| C | |||||||||
| B |
Это множество обладает одним и только одним гамильтоновым путем [2], которым является путь ADBFGCEH. Последнее означает, что наш друг Фреголи обладает одним и только одним способом одеться, как денди. Этот способ состоит в том, чтобы одеваться в таком порядке: галстук, жилет, носки, ботинки, пиджак, пальто, перчатки.
Некоторые аналогичные задачи могут привести к нескольким решениям; так, если бы в приведенном примере мы имели D  F, то существовало бы дополнительное решение ABDFGCEH.
F, то существовало бы дополнительное решение ABDFGCEH.
Хотя мы описали алгоритм Фаулкса на столь забавном примере, ясно, что он может быть также использован при решении гораздо более серьезных задач.
Задачи о назначении в промышленности, например, могут носить такой же комбинаторный характер: речь может идти о выполнении некоторого числа операций на различных машинах; при этом на порядок этих операций могут быть наложены условия с помощью связей типа <,  или |<. Когда имеется много машин и много операций, единственность решения встречается
или |<. Когда имеется много машин и много операций, единственность решения встречается

Рис. 16.2.

Рис. 16.3.
редко. В этих условиях остается выбрать, согласно определенному критерию (в качестве которого могут выступать затраты или длительность процесса), лучший из возможных порядков, даваемых решениями задачи.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 77; Нарушение авторских прав?; Мы поможем в написании вашей работы!