
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алгоритм Фаулкса
|
|
|
|
Рассмотрим шесть операций: А, В, С, D, E, F, между которыми существуют следующие соотношения:
А < В В |<С С <D Е < D F < D
A < D В < D F < E
A 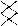 F B
F B 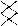 E
E
B 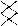 F
F
Цель задачи состоит в том, чтобы найти (если это возможно) пути, проходящие один и только один раз через каждую из точек и удовлетворяющие написанным соотношениям: это гамильтоновы пути.
|  Рис. 16.4.
Рис. 16.4.
|
Исследование графа, изображенного на рис. 16.4, показывает, что точка Dесть безусловно конечная точка каждого гамильтонова пути (если таковой существует), ибо никакая дуга не имеет эту точку своим началом, тогда как дуга, исходящая из любой другой точки, достигает точки D.
Это свойство выражается наличием единиц во всем столбце Dи нулей во всей строке D(очевидно, за исключением их пересечения).
Может наблюдаться и обратная ситуация: если для некоторой точки вся строка состоит из единиц и весь столбец, за исключением пересечения, состоит из нулей, эта точка является началом каждого гамильтонова пути (если таковой существует).
Матрицу графа можно упростить, вычеркивая предварительно все пары строк и столбцов, которым необходимо соответствует либо начало, либо конец каждого гамильтонова пути.
Так, в настоящем случае строка и столбец Dмогут быть заранее опущены; мы получаем матрицу М′. Образуем элементарные произведения элементов какой-нибудь строки (например, строки А ) на элементы какого-нибудь столбца (скажем, С), как если бы мы хотели вычислить М′[2].
| A | B | C | E | F | |
| A | |||||
| B | |||||
| C | |||||
| E | |||||
| F |
Элементарные произведения в порядке их следования таковы:
а) 1 · 0=0; б) 1 · 1 = 1; в) 0 · 1=0; г) 0 · 0=0; д) 1 · 0=0. Проследим, что они означают. Пусть мы хотим отправиться из A в С.
Тогда:
а) не существует прямого пути из A в C;
б) существует прямой путь, идущий из A в B, и путь из B в C; следовательно, имеется путь длины 2 из A в C;
в) не существует прямого пути из A в C;
г) нет прямого пути из A в E и также нет пути из E в C;
д) есть прямой путь из A в F, но нет никакого пути из F в С.
Таким образом, мы получили все пути из A в C длины меньшей или равной 2.
Так как мы ищем пути, связывающие различные точки графа, то вместо образования арифметической суммы, как в обычном матричном произведении, мы составим булеву сумму.
Таким образом, мы приходим к матрице М′[2], все единицы которой обозначают существование путей длины меньшей или равной 2, а нули — их отсутствие.
| М′[2]= | A | B | C | E | F | |
| A | ||||||
| B | ||||||
| C | ||||||
| E | ||||||
| F |
Из матрицы М′[2] мы заключаем, что точка Cнеобходимо является крайней точкой гамильтонова пути, если таковой существует. Опять отбрасываем строку и столбец C, откуда получаем
| М′′[2]= | A | B | E | F | |
| A | |||||
| B | |||||
| E | |||||
| F |
| М′′[3]= | A | B | E | F | |
| A | |||||
| B | |||||
| E | |||||
| F |
Точно так же, как мы, вычислив М′′[2], нашли пути длины меньшей или равной 2, найдем пути длины меньшей или равной 3, вычисляя М′′[3]. Матрица М′′[3] содержит только единицы; это доказывает существование путей длины меньшей или равной 3 между всеми точками ABEF, взятыми по две.
В частности, можно идти из Eв Aчерез Bи F. Вычислять М′′[4], которая, очевидно, содержит только единицы, уже нет смысла.
Вообще, когда вычисляют последовательные символические степени М, можно остановиться на том n, для которого
М[n+1]= М[n],
ибо это означает, что в М не существует пути, длина которого превышает п. Матрица М[3], полученная возвращением на место строк и столбцов C и D, может быть перегруппирована таким образом, чтобы все нули были расположены под главной диагональю, а единицы — над ней.
Квадратные матрицы, состоящие из единиц, опирающихся на главную диагональ, образуют классы эквивалентности относительно закона: точка X связана с точкой Yи обратно
| A | B | C | D | E | F | |
| A | ||||||
| B | ||||||
| C | ||||||
| D | ||||||
| E | ||||||
| F |
Например, А связана с Eчерез Bили через Fили же через FиB; Есвязана с A через Bи F. Мы упростим исходный граф, разбив его на классы. Определение единственного гамильтонова пути AFEBCDстановится совсем простым (рис. 16.5).

Рис. 16.5.
Возвращаясь к задаче Фреголи, которую мы решили выше, мы устанавливаем, что вычисление М[2] дало нам пути длины ≤ 2, вычисление М[4] — пути длины ≤ 4. Если бы мы вычислили М[7], мы имели бы пути длины ≤ 7; в действительности мы вычислили М[8], которая дает все пути, ибо каждый путь длины больше 7 проходит два раза через одну точку. Мы констатировали совпадение М[8] и М[4].
Затем мы нашли классы эквивалентности, представляя М[4] в форме ABDFGCEH; в частности, BDF и ЕН образуют классы эквивалентности.
Замечание. Очевидно, что когда записывают отношения порядка (как, например, отношения предшествования) в некотором множестве, алгоритм Фаулкса представляет собой один из методов выяснения их совместности (поскольку не должно существовать цикла). Он позволяет, кроме того, найти все отношения порядка между двумя элементами, которые выводятся из предположений в силу транзитивности отношения порядка (из А < В и В < С следует, что А < С, хотя это отношение не было явно выражено ранее).
Только тогда, когда между точками нет связи в виде отношения, можно вводить законно отношение индифферентности ><.
Зато на практике часто приходится иметь дело с соотношением частичного упорядочения, допускающим циклы. В этом случае этот алгоритм дает нам метод, хорошо приспособленный для решения задачи.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 168; Нарушение авторских прав?; Мы поможем в написании вашей работы!