
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Яка статистична характеристика визначається за формулою ?
|
|
|
|
Завдання 7.13
Завдання 7.12
Завдання 7.11
Завдання 7.10
Завдання 7.9
Завдання 7.8
Завдання 7.7
Завдання 7.6
Завдання 7.5
Завдання 7.4
Завдання 7.3
Завдання 7.2
Завдання 7.1
Необхідно:
– використовуючи дані таблиці 7.7 про споживання м’яса та м’ясопродуктів у сім’ях робітників і службовців залежно від рівня середньодушового сукупного доходу, за допомогою кореляційного відношення оцінити щільність зв’язку між названими показниками. Відомо, що загальна дисперсія споживання м’яса і м’ясопродуктів становить 12,9. Перевірити істотність зв’язку між цими ознаками з імовірністю 0,95.
Дані для виконання:
Таблиця 7.7. Дані про споживання м’яса та м’ясопродуктів у сім’ях робітників і службовців залежно від рівня середньодушового сукупного доходу
| Рівень середньодушового сукупного доходу | Кількість сімей, % до підсумку | Споживання м’яса і м’ясопродуктів на члена сім’ї за рік, кг |
| Низький | ||
| Середній | ||
| Високий | ||
| Разом |
Розв’язок. Результативною ознакою y є споживання м’яса і м’ясопродуктів, а факторною x – рівень середньодушового сукупного доходу. Для оцінки тісноти зв’язку між цими ознаками використовують відношення 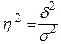 , де
, де 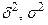 – міжгрупова і загальна дисперсія.
– міжгрупова і загальна дисперсія.
Міжгрупову дисперсію обчислюють за формулою:
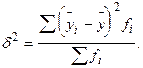
Розрахунок міжгрупової дисперсії подано в табл. 7.8.
Таблиця 7.8. Розрахунок міжгрупової дисперсії
| Номер груп за факторною ознакою | 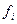
| 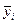
| 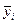 - - 
| (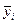 - -  )2 х )2 х 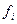
|
| ‑18 | ||||
| ‑2 | ||||
| Разом | ‑ |
Міжгрупова дисперсія становить  , а загальна
, а загальна 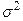 = 12,9, кореляційне відношення –
= 12,9, кореляційне відношення – 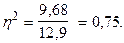
Це означає, що 75% варіації споживання м’яса і м’ясопродуктів залежить від рівня середньодушового сукупного доходу, 25 % припадає на долю інших ознак.
Істотність зв’язку перевіримо за допомогою F-критерію:
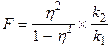 .
.
Число ступенів вільності можна визначити так:
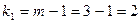 ,
,
 ,
,
де m – число груп за факторною ознакою; n – кількість елементів сукупності;

Фактичне значення F-критерію більше від критичного F0,95 (2; 97) = 3,11, тобто зв’язок між рівнем середньодушового сукупного доходу і споживанням м’яса та м’ясопродуктів з імовірністю 0,95 визнається істотним.
Необхідно:
– за даними табл. 7.9 обчислити параметри лінійного рівняння регресії, надати їм економічну інтерпретацію;
– за допомогою коефіцієнта детермінації визначити щільність зв’язку між урожайністю кукурудзи та строком її збирання;
– перевірити істотність зв’язку між зазначеними ознаками з імовірністю 0,95.
Дані для виконання:
Таблиця 7.9. Залежність урожайності кукурудзи від строку збирання урожаю обстежено 10 господарств, які належать до однієї природнокліматичної зони
| Номер господарства | Строк збирання урожаю, днів | Урожайність кукурудзи, ц/га |
Розв’язок. Результативною ознакою y є урожайність кукурудзи, а факторною x – строк збирання урожаю.
Для оцінки параметрів лінійного рівняння регресії складають систему нормальних рівнянь, що має вигляд:

Розрахункові суми для складання систем нормальних рівнянь наведено
в табл. 7.10.
Таблиця 7.10. Розрахунок сум для складання систем нормальних рівнянь
| № з/п | x | y | xy | х2 | y2 | Y | (Y -  )2 )2
|
| А | |||||||
| 32,60 | 43,56 | ||||||
| 40,64 | 2,07 | ||||||
| 50,69 | 132,02 | ||||||
| 46,67 | 55,80 | ||||||
| 36,62 | 6,66 | ||||||
| 26,57 | 159,52 | ||||||
| 38,63 | 0,33 | ||||||
| 18,53 | 427,25 | ||||||
| 54,71 | 240,56 | ||||||
| 46,67 | 55,80 | ||||||
| Разом | ‑ | 1123,57 |
Після підстановки відповідних значень х та у одержимо систему рівнянь:
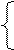 392 = 10 a + 237 b;
392 = 10 a + 237 b;
8731 = 237 a + 5895 b.
Після розв’язку цієї системи будь-яким способом знаходимо відповідні значення a та b, підставляємо їх до формули рівняння регресії, в результаті чого одержимо:
Y = 86,87 – 2,01 x.
При збільшенні строку збирання урожаю кукурудзи на один день її урожайність знижується в середньому на 2,01 ц/га.
На підставі рівняння регресії обчислюють теоретичні значення Y
для всіх елементів сукупності. Наприклад, для першого господарства
Y 1 = 86,87 – 2,01 х 27 = 32,6 ц/га.
Теоретичні значення Y використовують для обчислення коефіцієнту детермінації  , де
, де 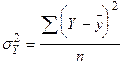 – факторна,
– факторна, 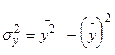 – загальна дисперсія.
– загальна дисперсія.
Отже, 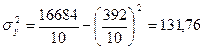 ;
; 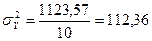 . Тоді
. Тоді 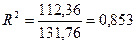 .
.
Таким чином 85,3 % варіації урожайності кукурудзи лінійно пов’язані зі строком збирання урожаю.
Перевірку істотності зв’язку здійснюють за допомогою F-критерію, або 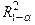 для ступенів вільнoсті:
для ступенів вільнoсті:
k 1 = m – 1 = 2 – 1 = 1;
k 2 = n – m = 10 – 2 = 8,
де m – число параметрів рівняння регресії для лінійного рівняння (m = 2), а n – кількість елементів сукупності (n = 10).
Критичне значення  для імовірності 0,95 згідно з додатком становить
для імовірності 0,95 згідно з додатком становить 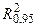 (1,8) = 0,399. Фактичне значення
(1,8) = 0,399. Фактичне значення  = 0,853 перевищує критичне, що свідчить про істотність зв’язку.
= 0,853 перевищує критичне, що свідчить про істотність зв’язку.
Необхідно:
– за результатами соціологічного опитування робітників-верстатників (таблиця 7.11) обчислити коефіцієнт асоціації, перевірити істотність зв’язку з імовірністю 0,95.
Дані для виконання:
Таблиця 7.11. Дані соціологічного опитування робітників-верстатників
| Чи задоволені ви темпами кваліфікаційного зростання | Чи маєте намір оволодіти суміжною професією | Разом | |
| так | ні | ||
| Так | |||
| Ні | |||
| Разом |
Розв’язок. Коефіцієнт асоціації обчислюють за формулою:
 ,
,
де  – частоти відповідних комбінацій ознак. За розрахунком коефіцієнт асоціації становить +0,46, що свідчить про наявність прямого зв’язку між темпами кваліфікаційного зростання і набуттям суміжних професій,
– частоти відповідних комбінацій ознак. За розрахунком коефіцієнт асоціації становить +0,46, що свідчить про наявність прямого зв’язку між темпами кваліфікаційного зростання і набуттям суміжних професій,
 .
.
Перевірку істотності зв’язку здійснюють за допомогою критерію 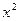 , статистична характеристика якого функціонально пов’язана з коефіцієнтом асоціації:
, статистична характеристика якого функціонально пов’язана з коефіцієнтом асоціації:
 .
.
Критичне значення 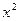 для рівня істотності a = 0,05 і числа ступенів вільності K = 1 становить
для рівня істотності a = 0,05 і числа ступенів вільності K = 1 становить 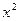 0,95 (1) = 3,84 (див. додаток).
0,95 (1) = 3,84 (див. додаток).
Фактичне значення  більше від критичного. Отже, зв’язок між темпами кваліфікаційного зростання і набуттям суміжних професій істотний.
більше від критичного. Отже, зв’язок між темпами кваліфікаційного зростання і набуттям суміжних професій істотний.
Необхідно:
– за даними табл. 7.12 обчислити коефіцієнт співзалежності; з імовірністю 0,95 перевірити істотність зв’язку між ознаками.
Дані для виконання:
Таблиця 7.12. Дані комбінаційного розподілу подружніх пар за віком, років
| Вік дружини | Вік чоловіка | Разом | ||
| 15–29 | 30– 44 | 45 і більше | ||
| 15–29 | ||||
| 30–44 | ||||
| 45 і більше | ‑ | |||
| Разом |
Розв’язок. Оскільки число груп за обома ознаками однакове, використовуємо формулу коефіцієнта співзалежності Чупрова:
 ,
,
де 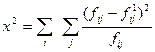 – сума стандартизованих відхилень фактичних частот розподілу від теоретичних; m1 та m2 – кількість груп за першою і другою ознаками; n – кількість елементів сукупності.
– сума стандартизованих відхилень фактичних частот розподілу від теоретичних; m1 та m2 – кількість груп за першою і другою ознаками; n – кількість елементів сукупності.
Розрахунок 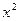 подано в табл. 7.13. Теоретичні частоти обчислюють на основі підсумкових частот
подано в табл. 7.13. Теоретичні частоти обчислюють на основі підсумкових частот 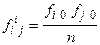 .
.
Наприклад, 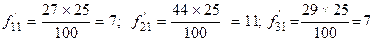 і т. д.
і т. д.
Таблиця 7.13. Розрахункова таблиця
| Група i j | f i j | f ‘i j | F i j – f ‘i j | (f i j – f ‘i j)2 | (f i j – f ‘i j)2 / f ‘i j |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 28,0 | |||||
| -6 | 3,3 | ||||
| -8 | 7,1 | ||||
| -7 | 4,4 | ||||
| 13,1 | |||||
| -5 | 8,0 | ||||
| -7 | 7,0 | ||||
| -7 | 4,1 | ||||
| 19,6 | |||||
| Разом | ‑ | 96,3 |
Коефіцієнт співзалежності становить 0,49, тобто:
 .
.
Перевірку істотності зв’язку здійснюють за допомогою критерію 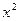 з числом ступенів вільності K = (m1 – 1) (m2 – 1) = 2 x 2 = 4.
з числом ступенів вільності K = (m1 – 1) (m2 – 1) = 2 x 2 = 4.
Критичне значення 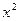 (0,95) (4) = 9,49 значно менше від фактичного
(0,95) (4) = 9,49 значно менше від фактичного  , отже, зв’язок між віком подружжя істотний.
, отже, зв’язок між віком подружжя істотний.
Необхідно:
– обчислити коефіцієнт рангової кореляції та перевірити істотність зв’язку між результатами лижників у кросах і лижних гонках з імовірністю 0,95.
Дані для виконання:
Підсумкові результати в кросах (ранг Х) і лижній гонці (ранг Y) у 10 лижників розподілились так:
| X | ||||||||||
| Y |
Розв’язок. Коефіцієнт рангової кореляції визначають за формулою Спірмена
 ,
,
де n – кількість елементів сукупності; d =  – відхилення рангів.
– відхилення рангів.
Розрахунок суми квадратів відхилень рангів наведено в табл. 7.14.
Таблиця 7.14. Розрахунок суми квадратів відхилень рангів
| X | Y | d = 
| d 2 |
| ‑ | ‑ | ‑ |
За розрахунком коефіцієнт рангової кореляції становить 0,83.
Критичне значення r для a = 0,05 наведено в додатку. Для n = 10 критичне значення r 0,95 = 0,563 менше від фактичного, що свідчить
про істотний зв’язок між ознаками.
Завдання для самопідготовки
Необхідно:
– визначити, яка з наведених нижче корельованих пар ознак є факторною, а яка результативною.
Дані для виконання:
1. Потужність електростанції, виробництво електроенергії.
2. Споживчі ціни, купівельна спроможність грошової одиниці.
3. Безробіття, рівень злочинності.
4. Продуктивність праці робітника-верстатника, вік виробничого обладнання.
5. Торгова площа магазинів, товарооборот.
6. Оборот біржі, кількість брокерських місць.
7. Фізичний знос обладнання, коефіцієнт змінності роботи підприємства.
Необхідно:
– визначити, які з наведених залежностей соціально-економічних явищ є функціональними, а які кореляційними:
Дані для виконання:
1. Витрати сімей на продукти харчування – від числа членів сім’ї.
2. Загальний капітал акціонерної компанії – від кількості випущених компанією акцій та їх ринкової ціни.
3. Тривалість життя населення регіону – від стану екологічного середовища.
4. Собівартість продукції – від обсягу виробництва і виробничих витрат.
5. Введення в дію житла – від капітальних вкладень у житлове будівництво.
6. Плата за кредит – від розміру позики і процента за користування кредитом.
7. Попит на товари народного споживання – від наявності їх на ринку і цін.
Необхідно:
– за даними табл. 7.15 обчислити: 1) міжгрупову дисперсію продуктивності верстатів; 2) за допомогою кореляційного відношення оцінити щільність зв’язку між виробітком деталей за зміну і строком служби верстатів; 3) використовуючи
F- критерій, перевірити істотність зв’язку з імовірністю 0,95.
Дані для виконання:
Загальна дисперсія продуктивності верстатів за зміну становить 292.
Таблиця 7.15. Дані про групування верстатів за строком служби
| Строк служби верстатів, років | Кількість верстатів | Виробіток деталей за зміну в розрахунку на 1 верстат, шт. |
| До 7 | ||
| 7–14 | ||
| 14–20 | ||
| 20 і більше | ||
| Разом |
Необхідно:
– за даними табл. 7.16: 1) обчислити міжгрупову, середню з групових та загальну дисперсії виробітку одного автомобіля, показати їх взаємозв’язок; 2) для оцінки тісноти зв’язку між виробітком автомобіля та його технічною швидкістю використати кореляційне відношення, пояснити його економічний зміст; 3) за допомогою F-критерію перевірити істотність зв’язку. Зробити висновки з імовірністю 0,95.
Дані для виконання:
Таблиця 7.16. Залежність виробітку вантажного автомобіля від технічної швидкості
| Середня технічна швидкість автомобіля, км/год. | Кількість автотранспортних підприємств | Середній виробіток на 1 машино-год, т-км | Дисперсія середнього виробітку |
| До 30 | |||
| 30–40 | |||
| 40–50 | |||
| 50 і більше | |||
| Разом | ‑ |
Необхідно:
1) визначити функцію, яка відображає залежність якості сировини
від дальності перевезень; 2) обчислити параметри рівняння регресії, пояснити їх економічний зміст; 3) за допомогою коефіцієнта детермінації оцінити щільність зв’язку між названими показниками; 4) перевірити істотність зв’язку, користуючись F -критерієм, з імовірністю 0,95, зробити висновки.
Дані для виконання:
Консервний комбінат здійснює заготівлю сировини в радіусі до 200 км (див. табл. 7.17).
Таблиця 7.17. Залежність якості заготовленої сировини від відстані перевезення
| Радіус перевезення, км | Частка нестандартної сировини, % | Радіус перевезення, км | Частка нестандартної сировини, % |
Необхідно:
– за даними табл. 7.18 оцінити щільність зв’язку між наведеними показниками за допомогою коефіцієнту асоціації; перевірити його істотність з імовірністю 0,95.
Дані для виконання:
Таблиця 7.18. Дані про стосунки 310 молодих сімей з батьками
| Молоді сім’ї, що проживають | Число молодих сімей, яким | ||
| допомагають батьки | не допомагають батьки | Разом | |
| З батьками | |||
| Окремо | |||
| Разом |
Необхідно:
– за даними табл. 7.19 проаналізувати комбінаційний розподіл робітників та оцінити щільність зв’язку між професійною мобільністю і задоволеністю працею за допомогою коефіцієнта співзалежності Чупрова; перевірити істотність зв’язку, використовуючи критерій  . Висновки зробити з імовірністю 0,95.
. Висновки зробити з імовірністю 0,95.
Дані для виконання:
Таблиця 7.19. Дані соціологічного опитування молодих робітників
| Чи задоволені професією | Чи маєте намір змінити професію | Разом | ||
| так, найближчим часом | так, в перспективі | ні | ||
| Задоволений | – | |||
| Ставлюсь байдуже | ||||
| Незадоволений | ‑ | |||
| Разом |
Необхідно:
– за даними табл. 7.20 оцінити щільність зв’язку між технічним і організаційним рівнями виробництва за допомогою коефіцієнта рангової кореляції; перевірити істотність зв’язків з імовірністю 0,95.
Дані для виконання:
Таблиця 7.20. Дані експертних бальних оцінок технічного і організаційного рівня виробництва груп промислових підприємств
| Номер підприємства | Рівень | |
| технічний | організаційний | |
| 1 | 2 | 3 |
Тестові завдання
для підсумкового контролю знань
7.1 Регресією називають:
а) будь-який причинно-наслідковий зв’язок між ознаками;
б) показник функціонального зв’язку між ознаками;
в) односторонню стохастичну залежність;
г) діаграму розсіювання.
7.2 Прямолінійним зв’язком називають зв’язок, коли:
а) результативна ознака пов’язана з однією факторною;
б) результативна ознака пов’язана з багатьма факторними;
в) його можна описати рівнянням прямої;
г) його можна описати рівняння кривої.
7.3 Стохастичний зв’язок це:
а) вид кореляційного зв’язку;
б) форма кореляційного зв’язку;
в) тип зв’язку між випадковими величинами;
г) зв’язок між випадковими величинами, при якому зміна однієї з них зумовлює зміну закону розподілу інших.
7.4 Кореляційний зв’язок, при якому значення результативної ознаки зменшується при збільшенні факторної ознаки називається:
а) прямим;
б) прямолінійним;
в) зворотним;
г) криволінійним;
7.5 До складу кореляційного аналізу не включаються наступні етапи роботи:
а) математично-економічне моделювання;
б) знаходження параметрів кореляційного рівняння;
в) визначення кореляції атрибутивних ознак;
г) оцінка й аналіз одержаних результатів.
7.6 Коефіцієнт кореляції це:
а) вимірник тісноти кореляційного зв’язку при лінійній залежності;
б) вимірник тісноти кореляційного зв’язку при криволінійній залежності;
в) вимірник тісноти кореляційного зв’язку;
г) вимірник тісноти зворотного кореляційного зв’язку.
а) коефіцієнт детермінації;
б) лінійний коефіцієнт кореляції;
в) коефіцієнт Спірмена;
г) кореляційне відношення.
7.8 Візуальний аналіз емпіричних даних, що відображають залежність між двома змінними дозволяє провести:
а) метод найменших квадратів;
б) кореляційне відношення;
в) лінійний коефіцієнт кореляції;
г) діаграма розсіювання.
7.9 Перевірка істотності зв’язку здійснюється за допомогою:
а) коефіцієнта асоціації;
б) критерія Фішера;
в) критерія Чупрова;
г) коефіцієнта Спірмена.
7.10 У випадках, коли ознакам явища, що спостерігається, не вдається однозначно приписати ті чи інші значення для вимірювання тісноти зв’язку використовують:
а) коефіцієнт детермінації;
б) кореляційне відношення;
в) лінійний коефіцієнт кореляції;
г) коефіцієнта Фехнера.
Проблемні напрями досліджень
для підготовки доповідей та реферативних робіт
1. Особливості застосування кореляційно-регресійного аналізу в бухгалтерському обліку та господарському контролі.
2. Застосування методів кореляційно-регресійного аналізу в діяльності підприємств.
3. Окремі питання кореляційно-регресійного аналізу: непараметричні методи вивчення зв’язків.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 275; Нарушение авторских прав?; Мы поможем в написании вашей работы!