Лекция 12. Транспортные задачи линейного программирования

Пример 11.1.

Составить двойственную задачу по отношению к задаче, состоящей в максимизации функции

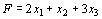(11.4)

при условиях

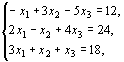(11.5)

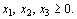(11.6)

Решение. Для данной задач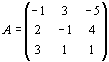и

и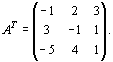

Число переменных в двойственной задаче равно числу уравнений в системе (11.5), т. е. равно трем. Коэффициентами в целевой функции двойственной задачи являются свободные члены системы уравнений (11.5), т.е. числа 12, 24, 18.

Целевая функция исходной задачи (11.4) – (11.6) исследуется на максимум, а система условий (11.5) содержит только уравнения. Поэтому в двойственной задаче целевая функция исследуется на минимум, а ее переменные могут принимать любые значения (в том числе и отрицательные). Так как все три переменные исходной задачи (11.4) – (11.6) принимают только лишь неотрицательные значения, то в системе условий двойственной задачи должны быть три неравенства вида “? ”. Следовательно, для задачи (11.4) – (11.6) двойственная задача такова: найти минимум функции 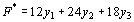при условиях

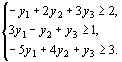
11.2.Решение задач линейного программирования с использованием программного обеспечения MATLAB

В состав MATLAB входит Optimization Toolbox, предназначенный для решения линейных и нелинейных оптимизационных задач.

Задача линейного программирования состоит в нахождении вектора x, который минимизирует целевую линейную функцию

f^Tx

при условии A X≤ B; X≥0,

где с =(с₁, c₂,…,c_n) представляет собой n-мерный вектор, соствленный из коэффициентов целевой функции, причем c^T – транспонированная вектор- строка; x=(x₁. x_n) – n –мерный вектор переменных решений,

B=[b₁

b₂ m-мерный вектор свободных членов

b_m]

B_eq=[b_eq1

_…

b_eqr] ограничения в виде равенств;

двусторонние покомпонентные ограничения в векторной форме

lb≤x≤ub

A=

Пример: задача состваления рациона питания

Имеются 3 продукта П₁, П₂ и П₃ разной цены, каждый из которых содержит определенное количество питательных ингридиентов И₁, И₂, И₃, И_4.

Известно, что в день требуется: И₁не менее 250, И₂ не менее 60, И₃ не менее 100 и И₄ не менее 220. Требуется минимизировать затраты на приобретение продуктов. Очевидно, что количество приобретаемых процессов не может быть отрицательным..

Записываем целевую функцию, матрицу A, векторы b и lb в соответствии с требованиями Toolbox, обозначив искомые количества продуктов через x_1, x₂ и x₃ соответственно. Поскольку линейные ограничения содержат «меньшк или равно», а количество ингредиентов в рационе не может быть менее заданных величин, то следует изменить знаки обеих частей системы.При вызове программы linprogвместо неиспользуемых ограничение (нет ограничений в виде равенств) задайте пустые массивы, обозначаемые в MATLAB пустыми скобками.

Программа ration

% задание матрицы и вектора правой части системы неравенств

A=[4 6 15

2 2 0

5 3 4

7 3 12]

A=-A;

b=[250 60 100 220];

b=-b;

% Определение коэффициентов целевой функции

f=[44; 35; 100];

% Задание ограничений снизу на переменные

lb=[0; 0; 0];

% решение и вывод результата в командное окно

x=linprog(f,A,b,[],[],lb)

Транспортная задача является представителем класса задач линейного программирования и поэтому обладает всеми качествами линейных оптимизационных задач, но одновременно она имеет и ряд дополнительных полезных свойств, которые позволили разработать специальные методы ее решения. Транспортная задача является одной из наиболее распространенных специальных задач линейного программирования. Частные постановки задачи рассмотрены рядом специалистов по транспорту, например О. Н. Толстым. Первая строгая постановка транспортной задачи принадлежит Ф. Хичкоку, поэтому в зарубежной литературе ее называют проблемой Хичкока.

Первый точный метод решения Т-задачи разработан Л. В. Канторовичем и М. К. Гавуриным. Под названием “транспортная задача” объединяется широкий круг задач с единой математической моделью. Данные задачи относятся к задачам линейного программирования и могут быть решены симплексным методом. Однако матрица системы ограничений транспортной задачи настолько своеобразна, что для ее решения разработаны специальные методы. Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его, получить оптимальное решение.

Дата добавления: 2017-02-01