Теоретические основы зарождения и роста покрытий из плазмы вакуумно-дугового разряда

Теория зарождения и роста покрытий основа на термодинамической теории Гибсса-Фольмера, которая учитывает термодинамические условия образования новой фазы. Под зарождением понимается возникновение зародышей новой фазы (твердой или жидкой) на поверхности Рост слоя происходит уже после возникновения зародышей за счет их увеличения и слияния с образованием сплошной пленки.

Структура образующейся пленки наследует то состояние, которое создалось при зарождении и последующем росте зародышей. Так большая частота зарождения и мелкие размеры зародышей способствуют образованию мелкозернистой структуры, и наоборот, малая частота зарождения и большие размеры зародышей приводят к созданию крупнозернистых пленок.

Рассмотрим термодинамическую модель зарождения и роста покрытий, учитывающую проведение процесса осаждения покрытий в условиях дополнительной ионной бомбардировки.

Возможны три варианта поведения атомов газовой фазы после соударения их с поверхностью подложки:

– атом адсорбируется на поверхности подложки;

– атом после адсорбции может реиспариться;

– атом может отражаться от поверхности.

То есть на первом этапе происходит столкновение атомов из газовой фазы с поверхностью подложки, после чего атомы могут прочно закрепиться на подложке, либо через некоторое время реиспариться, либо упруго отразиться от поверхности.

Вероятность упругого отражения может быть оценена как

, (6.21)

где E_k – кинетическая энергия атома падающего на подложку;

E_d – энергия десорбированного атома до установления термодинамического равновесия с подложкой;

E_T – энергия десорбированного атома после установления термодинамического равновесия с подложкой.

Величина a _i может быть приближенно определена из решения уравнения Шредингера для случая столкновения налетающего атома с одномерной полубесконечной упруго связанных атомов подложки.

Решение этого уравнения показало, что отражением падающих частиц можно пренебречь, если их энергия меньше, чем 25 E _д, где E _д– потенциальная энергия десорбции, что справедливо практически при всех методах получения пленок (для металлов, например,
E _д>>1 эВ, т.е. E_k должна быть не более 25 эВ). Кроме того, вероятность полной термической аккомодации (a_t = 1) увеличивается при увеличении отношения масс падающего атома и атома подложки. На основе той же модели было показано, что время релаксации энергии ~ 2/ n, где n – частота колебаний атомов подложки(n ~ 10¹¹-10¹³ с^–1). Таким образом, можно принять, что установление термо-динамического равновесия атомов с подложкой происходит мгновенно.

Адсорбированные атомы могут двигаться по поверхности (поверхностная диффузия) и при столкновении образовывать более устойчивые образования– начальные зародыши. Диффузия зародышей по поверхности, как правило, на много порядков меньше диффузии отдельных атомов и уменьшается по мере роста размеров зародыша. Поэтому считается, что зародыши на поверхности неподвижны. При достижении зародышами определенного размера соответствующего максимуму свободной энергии образования зародыша, он уже не распадается на отельные атомы, а растет, образуя устойчивый конденсат.

Наиболее вероятны первые два случая. Вероятность реиспарения адсорбированного атома определяется соотношением

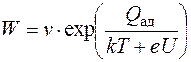, (6.22)

где n– частота колебаний адсорбированного атома (~ 10¹⁴ с^–1);

Q _ад – энергия связи адсорбированного атома с поверхностью, равная энергии активации десорбции (отрицательная величина);

k – постоянная Больцмана;

Т – температура адсорбированных атомов;

e – заряд электрона;

U – разность потенциалов.

Отношение 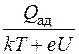определяет время жизни адсорбированного атома на поверхности. Если адсорбированные атомы приходят в соотношение теплового равновесия сразу после соударения, величина Т = Т _подл.

Если Q _ад>>(kT + eU), вероятность реиспарения очень мала. Это условие выполняется при очень низких температурах Т _подл или при осаждении металла на металлическую подложку, когда Q _ад имеет очень большую величину.

Если подложка инертна по отношению к атомам пленки (стекло, пластмасса и др.), то Q _ад очень мала и вероятность реиспарения в условиях дополнительной ионной бомбардировки окажется высокой. Число реиспарившихся атомов будет определяться соотношением

, (6.23)

где N ↑– число реиспарившихся атомов с 1 см² поверхности в 1 с;

N _ад – число атомов, адсорбированных на 1 см² поверхности;

N _рас – число распыленных атомов с 1 см² поверхности.

Если N ↑= N ↓, то осуществляется стационарное состояние и заполнение подложки является функцией скорости осаждения N ↓, т.е.

(6.24)

При высоких скоростях поступления атомов на подложку необходимо учитывать взаимодействие между адсорбированными атомами. Адсорбированные атомы мигрируют по поверхности, образуют скопление адсорбированных атомов (зародышей). Процесс зародышеобразования заключается в возникновении и росте агрегатов молекул в результате протекания реакций по схеме, представленной ниже.

m₁+ m₁Dm₂,

m₂+ m₁Dm₃, (6.25)

_{…………………}

m _n + m₁Dm _{n +1}.

Образование зародыша новой фазы, содержащего n молекул, сопровождается изменением свободной энергии , связанным с появлением определенного объема второй фазы и поверхности раздела фаз.

При малых размерах зародыши обладают высокой поверхностной энергией, что делает их менее стабильными, так как большая величина поверхностной энергии приводит к увеличению давления пара над поверхностью по сравнению с массивным конденсатом и, следовательно, к диссоциации этих скоплений. Поэтому должны существовать критические размеры зародышей, при которых они обладают минимальной устойчивостью. Добавление атомов к зародышам критического размера повышает устойчивость таких скоплений. Вычислим размер критического зародыша r _кр. Если при конденсации возникает зародыш с изотропной поверхностной энергией, то можно предположить, что он будет иметь куполообразную форму (рис. 6.9.)

Рис. 6.9. Схема зародышеобразования:

1 – газовая фаза; 2 – подложка; 3 – зародыш

Тогда полная свободная энергия зародыша G определяется соотношением

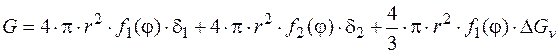, (6.26)

где r – радиус кривизны зародыша;

d₁; d₂; d₃ – удельные межфазовые свободные энергии поверхностей раздела конденсат-пар, конденсат-подложка и пар-подложка, соответственно;

f ₁(j); f ₂(j); f ₃(j) – геометрический фактор, зависящий от величины контактного угла;

– удельное изменение свободной энергии при образовании конденсата.

Современные теоретические представления описывают три возможных режима роста тонких пленок после образования начальных устойчивых зародышей: послойный, островковый и смешанный. Реализация в конкретной системе того или иного механизма роста определяется соотношением удельных свободных энергий границ раздела «пар-конденсат» (d₁), «конденсат-подложка» (d₂) и поверхности подложки (d₃).

В случае происходит послойный рост, т.е. последовательное заполнение подложки моно атомными слоями. При этом необходимо, чтобы указанное условие удовлетворялось после образования первого слоя (т.е. когда d₃ свободная энергия поверхности пленки). При происходит островковый рост. В этом случае связь атомов в островках больше чем с атомами поверхности подложки, что приводит к преимущественному росту островков вверх.

Величина контактного угла jопределяется равновесием свободных энергий по уравнению Гиббса

(6.27)

Удельное изменение свободной энергии при конденсации может быть определено по соотношению

, (6.28)

где V – молекулярный объем. Подставив вместо функции скорости осаждения выражение (6.1) получим и, представив количество частиц, падающих на поверхность, адсорбированных частиц и распыленных, соответственно, как

; (6.29)

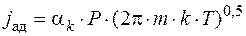, (6.30)

, (6.31)

, (6.32)

График уравнения (6.26) для различных температур представлен на рис. 6.9.

На начальной стадии образования зародышей будет сопровождаться увеличением свободной энергии до определенного значения G _кр при r = r _кр. Дальнейший рост зародышей приводит к уменьшению G. Зародыши с радиусом r < r _кр считаются нестабильными, а r > r _кр – стабильными.

Рис. 6.9. Зависимость свободной энергии изотермического образования
зародыша от размера зародыша для различных температур конденсации T ₀ > T ₁ > T ₂ > T ₃

Свободную энергию G _кр критического зародыша получим, найдя максимум уравнения (6.26)

, (6.33)

, (6.34)

Размер критического зародыша r _кропределяется соотношением

. (6.35)

Функция контактного угла , представленная на рис. 6.10. характеризует взаимодействие конденсата с подложкой.

Рис. 6.10. Функция контактного угла f ₄(j) для куполообразного зародыша

При j®0, f ₄(j)®0, G _кр®0, т.е. образование зародышей облегчается. При j®180°, f ₄(j)®1, G _кр растет до максимумам и образование зародышей затрудняется.

Критические зародыши могут расти либо за счет атомов газовой фазы, либо за счет адсорбированных атомов, диффундирующих по поверхности подложки. Если критическими зародышами покрыта небольшая площадь, то преобладающим является рост за счет адсорбированных атомов; вероятность такого роста зависит от коэффициента диффузии адсорбированных атомов. В этом случае скорость роста зародышей определяется числом исходных зародышей на единице площади и скоростью присоединения к ним отдельных адсорбированных атомов. При условии равновесия число критических зародышей на единице поверхности подложки в условиях дополнительной ионной бомбардировки определяется выражением

, (6.36)

Скорость присоединения адсорбированных атомов к зародышам будет зависеть от числа адсорбированных атомов, частоты их перескоков, длины перескоков

, (6.37)

Где С – константа, в которую входят величины критического зародыша и другие геометрические факторы;

Q_D – энергия активации поверхностной диффузии адсорбированных атомов.

Из соотношений (6.24), (6.36), (6.37) можно получить выражение для числа минимального сверхкритического размера, возникающих на единице поверхности в единицу времени

(6.38)

Частота зарождения J сильно зависит от энергетических характеристик процесса зарождения пленки и, следовательно, от условий осаждения.

В первую очередь величина r _кр зависит от природы вещества пленки и подложки, температуры подложки, скорости осаждения, энергии активации поверхности, диффузии и энергии связи пленки с подложкой.

Рассмотрим зависимость размера критического зародыша от природы вещества пленки. Так как металлы с высокой температурой кипения обладают большим значением величины D G _n, то следует ожидать, что для металлов W, Mo, Ta, Ni и т.д. даже очень малые зародыши являются стабильными. Увеличение размера очень резко повышает устойчивость таких зародышей и делает диссоциацию и реиспарение маловероятным.

Размер зародышей резко уменьшается, если подложка имеет сильное сродство с веществом пленки или сама подложка обладает высокой свободной энергией. Так, если в качестве подложки используется металл, D G _ад»– 3Дж/м³ и d₃» 1Дж/м², то для конденсации серебра при Т =300К и N ↓ = 1Å/c критический размер зародыша имеет размер r _кр<0. Поэтому при осаждении металлов на металлическую подложках часто не существует энергетического барьера и, следовательно, можно ожидать образование сплошных пленок после нанесения нескольких моноатомных слоев.

Рассмотрим влияние температуры подложки на размеры критического зародыша. Дифференцируя (6.35) по температуре, получим

(6.39)

Используя типичные средние значения для металлов: d» 1Дж/м², , получим

, (6.40)

если D G _n < 1,64×10¹⁰ Дж/м³,что имеет место практически во всех случаях, когда имеется барьер зарождения. Следовательно, повышение температуры подложки при постоянной скорости осаждения приводит к увеличению размера критического зародыша.

Аналогично, дифференцируя G _кр по температуре, получим

(6.41)

Так как частота зарождения экспоненциально связана с величной D G _{n кр} скорость возникновения агрегатов сверхкритиче-ского размера быстро уменьшается с увеличением температуры. Зависимость r _крD G _крот скорости осаждения обусловлена тем, что скорость осаждения в сильной степени влияет на величину D G _n.

Поскольку энергия свободной поверхности и поверхности раздела не зависит от N↓, то

, (6.42)

. (6.43)

То есть увеличение скорости осаждения приводит к уменьшению размеров зародышей и к увеличению скорости их возникновения. Так как D G _nот N ↓ зависит логарифмически, небольшие изменения N ↓ (в 2-3 раза) не будут существенно влиять и менять r _кр. Для заметного изменения r _кр необходимо, чтобы N изменилось на несколько порядков.

Влияние поверхностной диффузии и энергии связи пленки с подложкой на размер критического зародыша определяется тем фактором, что коэффициенты диффузии атомов металла по поверхности подложки не влияют на размер зародыша. Однако скорость образования зародышей зависит от способности адсорбированных атомов диффундировать и сталкиваться друг с другом.

Действительно, согласно выражению (6.33) эта скорость уменьшается экспоненциально с увеличением энергии активации диффузии.

Если энергия активации поверхностной диффузии очень велика, диффузия будет происходить медленно и зародыши могут расти только за счет непосредственного столкновения с ними атомов паровой фазы. Энергию активации диффузии при адсорбции металлов на металл можно приблизительно считать равной 1/4 энергии активации десорбции в газовую среду, т.е. 0,25 (– Q _ад).

Величина энергии связи адсорбированных атомов с подложкой сильно влияет на величины r _кр и D G _кр. При увеличении Q _ад размеры критического зародыша уменьшаются, частота зарождения увеличивается. Высокой прочностью связи отличаются ступеньки на поверхности подложки.

В вакуумно-плазменной технологии используются покрытия, реальная толщина которых много больше, чем размеры зародышей.

При рассмотрении роста покрытия необходимо ответить на следующие вопросы:

– какое влияние оказывает механизм зарождения на структуру покрытия, на образование дефектов структуры, границ зерен, дефектов упаковки, вакансий, дислокаций и др.;

– какое влияние оказывает механизм роста на изменение и повторение структуры, повторившейся в процессе зарождения.

Какое влияние оказывают параметры технологического процесса на обеспечение заданных эксплуатационных свойств покрытий.

Характер дефектов и причины их возникновения в монокристаллических пленках являются типичными для любых покрытий – как монокристаллических, так и поликристаллических.

Модель осаждения монокристаллических пленок на монокристаллическую подложку (эпитаксия) может быть применима и к модели роста покрытия.

Независимо от исходной подложки, после того как получен первый сплошной слой пленки, механизм зарождения на этой пленке изменяется. Для анализа используем модель образования куполообразного зародыша, описанную выше.

Согласно уравнению (6.3) свободная энергия образования зародыша равна

, (6.44)

Но при осаждении слоя на предыдущий слой того же материала значение контактного угла равнаj= 0, тогда f ₄(j)= 0 и D G _кр= 0. Следовательно, энергетический барьер отсутствует, т.е. отсутствует система зародышей, и конденсирующиеся атомы на поверхности непосредственно включаются в структуру растущего кристалла.

Таким образом, после возникновения сплошной пленки ее рост следует рассматривать с позиции роста кристаллов. Механизм этого роста включает адсорбцию атомов из паровой фазы, поверхностную диффузию в ступеньке, взаимодействие со ступенькой, диффузию вдоль ступеньки и присоединение к кристаллу (рис. 6.11).

Рис. 6.11. Схематическое изображение поверхности кристалла
с частично заполненным одноатомным слоем:

1 – адсорбированный атом; 2 – атом, взаимодействующий со ступенькой
и диффундирующий вдоль нее; 3, 4 – атомы, закрепленные на ступеньке;
5 – атом в поверхностном слое.

Равновесия, которые существуют между различными положениями атомов, таковы

(6.45)

Здесь N – концентрация атомов соответствующего типа; P _me – давление паров; V_i – скорость указанных стадий процесса.

Скорость каждой из стадий процесса можно описать уравнениями

; (6.46)

; (6.47)

; (6.48)

; (6.49)

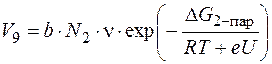; (6.50)

, (6.51)

где b – длина ступеньки на единице площади;

n– частота колебаний атомов, находящихся на поверхности (около 10¹³ с^–1);

P_w – вероятность данного направления движения атомов (1/6 для плотноупакованных плоскостей);

N ₀ – число позиций атомов на единичной поверхности и длине ступеньки;

N ₁ – равновесие концентрации атомов в молях;

D G_v – свободная энергия соответствующей стадии;

е – заряд электрона;

U – разность потенциалов.

Задача о росте пленки сводится к выявлению преобладающей стадии при тех или иных условиях. Например, когда преобладает поверхностная диффузия V ₂, уравнение непрерывности для адсорбированных атомов примет вид

, (6.52)

где N ₁ – концентрация адсорбированных атомов;

Х – координата движения частицы.

При росте в реальном технологическом процессе появляются дефекты кристаллической решетки: дислокации, дефекты упаковки, точечные дефекты. Причина появления дефектов многообразны. Так, ранее осажденные слои могут покрываться следующими до того, как будет достигнуто термическое равновесие с предыдущем слоем. При этом в слой может захватываться большое число вакансий. При низкой температуре подложки атомы будут оставаться в тех местах, куда они попали при соударении с поверхностью, и будут вносить разупорядоченность в структуру осаждаемой пленки. Этот процесс будет стимулироваться наличием предыдущего слоя, низкой температурой конденсации и т.д.

Концентрация дефектов условно характеризуется плотностью дислокаций, измеряемой числом их на 1 см². Эта величина в покрытиях металлов может достигать нередко значений 10¹⁰-10¹¹ см^–2.

Размер зерна конденсированного покрытия в переходной зоне и средней части помимо условий конденсации зависит от способа предварительной обработки поверхности и уровня шероховатости подложки. Микронеровности на поверхности определяют число активных центров роста конденсирующей пленки. Так, применение специальной жидкостно-абразивной обработки поверхностей деталей дисперсным корундом позволяет снизить уровень микронеровностей на жаропрочных сплавах до 1 мкм и менее. После абразивной обработки лопаток из сплава И-50 при Т _кон = 875°С размер зерна в покрытии Fe – 25 %, Cr – 6 %, А-V составляет 3-10 мкм.

Дата добавления: 2017-02-01