Шунтирование электроизмерительных приборов. Добавочные сопротивления к электроизмерительным приборам

Параллельное соединение сопротивлений

Пусть два проводника с сопротивлениями R₁ и R₂ соединены параллельно
(рис. 6.7). Признаком параллельного соединения является разветвление тока. В данном случае электрический ток I, входя в группу проводников с R₁ и R₂, разветвляется на два тока I₁ и I₂. Из закона сохранения зарядов следует, что ток I равен сумме токов I₁ и I₂:

. (6.35)

Напряжение на проводниках одинаково, поэтому можно записать

(6.36)

или

. (6.37)

Из формулы (6.37) следует:

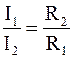. (6.38)

При параллельном соединении сопротивлений токи в отдельных проводниках обратно пропорциональны их сопротивлениям.

Для определения полного сопротивления цепи воспользуемся соотношением

, (6.39)

где R – полное сопротивление цепи.

Таким образом,

. (6.40)

Общая проводимость такого соединения проводников равна сумме проводимостей каждого из ветвей:

. (6.41)

Если параллельно соединены не два, а n проводников, то общая проводимость такого соединения

. (6.42)

При параллельном соединении n проводников с одинаковыми сопротивлениями общее сопротивление цепи

. (6.43)

В реальных электрических цепях встречаются как последовательное, параллельное соединение проводников (сопротивлений), так и смешанное (рис. 6.8). Для смешанного соединения сопротивлений справедливы законы ранее рассмотренных соединений.

Последовательное и параллельное соединения сопротивлений применяются в устройстве различных электроизмерительных приборов.

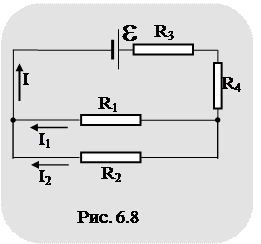
Например, гальванометр (электроизмерительный прибор высокой чувствительности для измерения малых токов, напряжений и количества электричества) рассчитан на измерение тока не выше предельного значения, указанного на шкале прибора. Для расширения предела измерения к зажимам гальванометра присоединяют параллельно проводник с малым сопротивлением, называемый шунтом (рис. 6.9).

Обозначим сопротивление гальванометра через R, а сопротивление шунта – через r. Пусть R в n раз больше, чем r, т.е. R/r = n. Токи в цепи, в гальванометре и в шунте обозначим через I, I_g, I_r. Тогда, согласно выражению (6.38),

; .

Полный ток в цепи

.

Откуда

. (6.44)

Таким образом, ток в гальванометре в (n + 1) раз меньше, чем ток в общей цепи. Тем самым благодаря шунту с помощью гальванометра можно измерять токи в (n + 1) раз большие, чем те, на которые он рассчитан, при этом цена деления прибора увеличивается в (n + 1) раз.

Использовать гальванометр для измерения напряжения возможно, если к нему последовательно присоединить добавочное сопротивление. Обозначим сопротивление гальванометра через R, а добавочное сопротивление – через r. Пусть r в n раз больше R, т.е. r/R = n. Тогда общее напряжение на добавочном сопротивлении и сопротивлении гальванометра (рис. 6.10)

(6.45)

Величина IR = U_g - напряжение на гальванометре. Следовательно, можно записать

. (6.46)

Следовательно, напряжение на гальванометре будет в (n + 1) раз меньше измеряемого. Тем самым, благодаря добавочному сопротивлению, с помощью гальванометра можно измерять напряжения в (n + 1) раз большие, чем те, на которые он рассчитан. При этом цена прибора увеличивается в (n + 1) раз.

Надо отметить, что применять шунты и добавочные сопротивления можно не только к гальванометрам, но и к другим приборам (амперметрам, вольтметрам) с целью расширения их пределов измерения.

6.4. Правила (законы) Кирхгофа
и их применение к расчету простейших электрических цепей

Закон Ома позволяет рассчитывать электрические цепи, в которых все элементы (проводники) соединены последовательно и в которых существует один и тот же ток.

На практике чаще всего встречаются электрические цепи с большим количеством разветвлений, токи в которых неравны (разветвленные электрические цепи).

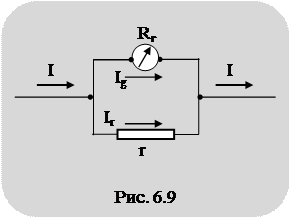
Для упрощения расчетов таких цепей пользуются правилами (законами) Кирхгофа (1847 г.). Рассмот-рим произвольную цепь, состоящую из нескольких проводников и источников тока (рис. 6.11).

Будем называть все точки, в которых сходятся не менее трех токов (проводников) узловыми точками или узлами (¢A¢ и ¢B¢). Участки цепи между узлами – ветвями (например, AE₁R₁R₄B), а участки цепи, состоящие из нескольких ветвей и образующие замкнутую цепь, – контурами (например, AE₁R₁R₄BE₂R₂A).

Условимся считать подходящие к узлу токи положительными токами, отходящие - отрицательными. Введя данные определения, сформулируем законы Кирхгофа:

· Первый закон: Алгебраическая сумма токов, сходящихся в узле, равна нулю, т. е.

. (6.47)

В нашем случае для узла ¢A¢

. (6.48)

При решении задач на основании первого закона Кирхгофа можно составить (n – 1) уравнение, где n – число узлов. Так как число узловых точек всегда меньше числа неизвестных величин, то для их определения составляют ряд дополнительных уравнений, пользуясь вторым законом Кирхгофа.

· Второй закон: Алгебраическая сумма падений напряжений на отдельных участках замкнутой цепи (замкнутого независимого контура) равна алгебраической сумме ЭДС, действующих в них, т. е.

. (6.49)

На основании второго закона Кирхгофа составляют (m – 1) уравнение, где m – число независимых контуров, т.е. таких, которые содержат хотя бы один элемент, не входящий в предыдущие контуры. В рассматриваемом случае число независимых контуров равно 3. Выбирается (произвольно) направление обхода контура. Ток, совпадающий по направлению с направлением обхода контура, считают положительным, а не совпадающий – отрицательным. ЭДС, действующую внутри контура, считают положительной, если при обходе контура внутри её происходит повышение потенциала (от минуса к плюсу), в противном случае – отрицательной. Падение напряжения на участке цепи считают положительным, если направление тока на нем совпадает с направлением обхода контура.

В рассматриваемом случае для независимого контура AE₁R₁R₄BE₂R₂A (без учета падения напряжения на внутреннем сопротивлении источников тока)

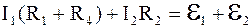. (6.50)

Для независимого контура AR₂E₂E₃R₃A (без учета падения напряжения на внутреннем сопротивлении источников тока)

. (6.51)

Таким образом, в рассматриваемом случае имеем систему уравнений

(6.52)

Решая систему уравнений (6.52), можно определить неизвестные, заданные условием задачи.

Надо отметить, что первоначальный выбор направлений токов и обхода контуров не играет никакой роли. После проведения расчетов значение токов будет получено со знаком, при этом знак "плюс" будет соответствовать правильному выбору направления тока в элементе цепи, "минус" – обратному.

6.5. Закон Джоуля-Ленца в дифференциальной
и интегральной формах

Двигаясь под действием силы F = e E, электрон проводимости приобретает некоторую энергию

. (6.53)

Провзаимодействовав с ионом кристаллической решетки, он отдает ему эту энергию, которая выделяется в проводнике в виде тепла.

Если взаимодействие электрона проводимости с ионом кристаллической решетки происходило в течение времени t, то за это время в проводнике выделится в виде тепла энергия

, (6.54)

где – число взаимодействий электрона проводимости с ионом кристаллической решетки.

Так как

то

, (6.55)

где – время свободного пробега электрона проводимости.

Если в объеме проводника содержится n электронов проводимости, то энергия, переданная единице объема проводника в единицу времени всеми электронами,

. (6.56)

Выражение (6.56) является математической формой записи закона Джоуля-Ленца в дифференциальной форме.

Из формулы (6.56) можно получить формулу закона Джоуля Ленца в интегральной форме. Имеем

,

где g = 1/r; E = U/dl, dV = S dl.

Следовательно,

или

, (6.57)

где - сопротивление проводника;

U = IR – напряжение.

Количество тепла, выделившееся в проводнике за время t,

. (6.58)

Выражение (6.58) является математической формой записи закона Джоуля-Ленца в интегральной форме.

В случае постоянного тока

. (6.59)

Классическая электронная теория проводимости металлов смогла объяснить не только электропроводность металлов и сплавов, но и их теплопроводность, некоторые оптические свойства вещества, что является её крупным достижением. Однако с её помощью невозможно объяснить такие экспериментальные факты, как независимость теплоемкости металлов от наличия электронов проводимости и сверхпроводимости. Это связано с тем, что в ней электроны проводимости подчиняются законам идеального газа, законам статистики Максвелла-Больцмана. В действительности же для электронов проводимости справедлива квантовая статистика, и они подчиняются закону статистики Ферми-Дирака.

6.6. Энергия, выделяющаяся в цепи постоянного тока. Коэффициент полезного действия (КПД)
источника постоянного тока

На участке цепи, не содержащей ЭДС, силы электрического поля совершают работу по перемещению электрического заряда, которая выделяется в проводнике в виде тепла:

. (6.60)

Если в цепи имеется ЭДС, то работа по перемещению электрического заряда совершается сторонними и электрическими силами, численно равная энергии, выделяющейся в этой цепи:

. (6.61)

В замкнутой цепи энергия, выделяющаяся в проводнике численно равна работе:

. (6.62)

Таким образом, в замкнутой цепи внутри источника сторонние силы совершают работу по разделению зарядов, создают электрическое поле и запасают энергию, которая расходуется во внешней цепи на поддержание электрического поля, или выделяется в виде тепла. В замкнутой цепи совершают работу только сторонние силы.

Известно, что работа, совершаемая в единицу времени, называется мощностью:

. (6.63)

Это оказывается справедливым и для постоянного электрического тока. Поэтому для участка цепи, в котором отсутствует ЭДС, мощность

. (6.64)

При наличии ЭДС

. (6.65)

В замкнутой цепи

. (6.66)

Мощность во внешней цепи является полезной мощностью

. (6.67)

Отношение полезной мощности (мощности во внешней цепи) к мощности, развиваемой источником тока (полной мощности), называют коэффициентом полезного действия (КПД):

. (6.68)

Из выражения (6.67) видно, что при r®0, h®1.

Найдем соотношение между R и r, при котором полезная мощность максимальна. Для этого проведем исследование функции P_вн = f(R). Определяем первую производную и приравниваем её к нулю:

. (6.69)

Определяем вторую производную и исследуем её знак:

. (6.70)

Из формул (6.64) и (6.65) видно, что в том случае, когда сопротивление внешнего участка цепи равно внутреннему сопротивлению источника тока (R = r), мощность во внешней цепи максимальна:

. (6.71)

При этом коэффициент полезного действия (при максимальном значении мощности во внешней цепи)

. (6.72)

Можно установить зависимость КПД источника тока от тока во внешней цепи (h = f (I)):

. (6.73)

Графики зависимости мощности во внешней цепи, полной мощности и коэффициента полезного действия источника тока от тока в цепи представлены на рис. 6. 12. Зависимость КПД от сопротивления внешнего участка цепи h = f(R)

. (6.74)

Из вышеизложенного видно, что получение P_max и h_max невозможно, т.к. при P_вн = P_max, h = 0,5, а при h®1, P_вн®0.

Лекция 7. Электрический ток в вакууме,
газах и жидкостях

Электрический ток в вакууме. Термоэлектронная эмиссия. Вторичная и автоэлектронная эмиссия. Электрический ток в газе. Процессы ионизации и рекомбинации. Несамостоятельная и самостоятельная проводимость газов. Теория Таунсенда. Закон Пашена. Виды разрядов в газах. Понятие о плазме. Плазменная частота. Дебаевская длина. Электропроводность плазмы. Электролиты. Электролиз. Законы электролиза. Электрохимические потенциалы. Электрический ток через электролиты. Закон Ома для электролитов. Применение электролиза в технике.

Дата добавления: 2017-02-01