
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Электрический ток в вакууме. Термоэлектронная эмиссия
|
|
|
|
Вакуум – это состояние газа при давлении меньше атмосферного. Степень вакуума определяют, измеряя величину давления остаточных газов.
Физической характеристикой вакуума является соотношение между длиной свободного пробега l молекул газа и размером d, характерным для каждого конкретного процесса или прибора (расстояние между стенками вакуумной камеры, диаметр вакуумного трубопровода, расстояние между электродами электровакуумного прибора и т.п.).
Величина l равна отношению средней скорости v молекулы к числу z столкновений, испытываемых молекулой за единицу времени. Длину свободного пробега можно выразить через радиус молекулы r и число молекул n в единице объема:
 . (7.1)
. (7.1)
В зависимости от величины отношения  различают низкий вакуум (
различают низкий вакуум ( <<1), средний вакуум (
<<1), средний вакуум ( ~1), высокий вакуум (l>>1) и сверхвысокий вакуум.
~1), высокий вакуум (l>>1) и сверхвысокий вакуум.
Понятие сверхвысокого вакуума связано не с величиной отношения  , а со временем t, необходимым для образования мономолекулярного слоя газа на поверхности твердого тела в вакууме, которое обратно пропорционально давлению.
, а со временем t, необходимым для образования мономолекулярного слоя газа на поверхности твердого тела в вакууме, которое обратно пропорционально давлению.
Свойства газа в низком вакууме определяются частыми столкновениями между молекулами газа в объеме, сопровождающимися обменом энергией. Поэтому течение газа в низком вакууме носит вязкостный характер, а явления переноса (теплопроводность, внутреннее трение, диффузия) характеризуются плавным изменением (или постоянством) градиента переносимой величины.
В высоком вакууме поведение газа определяется столкновениями его молекул со стенками или другими твердыми телами. Столкновения молекул друг с другом происходят редко и играют второстепенную роль. Движение молекул между твердыми поверхностями происходит по прямолинейным траекториям (молекулярный режим течения). Явления переноса характеризуются скачком переносимой величины на границе. Количество переносимой величины (теплоты) прямо пропорционально давлению p. Прохождение тока в высоком вакууме возможно в результате электронной эмиссии с электродов.
Свойства газа в среднем вакууме являются промежуточными.
В атомах металла свободные электроны при обычных температурах не могут покинуть металл. Из этого следует, что металл относительно окружающего его вакуума должен иметь положительный потенциал, которым и удерживаются в нем свободные электроны.
Положительный потенциал j внутренней части металла относительно вакуума называется внутренним потенциалом.
Потенциальная энергия свободного электрона внутри металла определяется произведением заряда электрона (-e) и внутреннего потенциала:
 . (7.2)
. (7.2)
 Так как j>0, то W<0. Таким образом, потенциальная энергия электрона в металле относительно вакуума отрицательна.
Так как j>0, то W<0. Таким образом, потенциальная энергия электрона в металле относительно вакуума отрицательна.
Свободные электроны металла можно приближенно считать заключенными в "потенциальную яму с плоским дном" (рис. 7.1).
Картина изменения потенциальной энергии, изображенная на рис. 7.1а, является приближенной. В решетке металла происходит периодическое распределение зарядов в виде положительных ионов и окружающих их облаков отрицательного заряда, и поэтому потенциальная энергия периодически изменятся в пространстве. Она принимает наименьшие значения в местах нахождения положительных ионов и наибольшие – в промежутке между ними (рис. 7.1,б). Представляя металл в виде потенциального ящика с плоским дном, можно заменить периодический потенциал его средним значением, что оказывается вполне допустимым приближением при рассмотрении явлений электронной эмиссии.
Чтобы вырвать свободный электрон из металла, необходимо произвести определенную работу, равную глубине потенциальной ямы металла:
 . (7.3)
. (7.3)
Эта работа называется работой выхода электрона из металла.
Для различных металлов работа выхода колеблется в пределах от 1 до 5 эВ.
Условие, при котором электрон может покинуть металл, имеет вид
 , (7.4)
, (7.4)
где m – масса электрона;
vn – проекция скорости электрона на направление нормали к поверхности металла.
Выход свободных электронов из металла называется эмиссией электронов. Эмиссия электронов может происходить под влиянием различных факторов: в результате ударов частиц (электронов и ионов) о поверхность металла (вторичная эмиссия); воздействия падающего на металл света (фотоэмиссия); в результате теплового движения свободных электронов.
Эмиссия электронов, порождаемая их тепловым движением, называется термоэлектронной эмиссией.
С точки зрения классической физики, термоэлектронную эмиссию можно представить следующим образом. При высоких температурах средняя кинетическая энергия свободных электронов, характеризуемая величиной kT, становится соизмеримой с работой выхода их с поверхности металла, поэтому часть этих электронов покидает металл и образует вокруг него электронное облако. Электронное облако своим пространственным отрицательным зарядом создает электрическое поле с потенциалом, который в общем случае является функцией координат.
Если электронное облако и металл поддерживаются в равновесном состоянии при температуре T K, то число вылетающих электронов из металла равно числу электронов, попадающих из электронного облака в металл за тот же промежуток времени.
Поэтому в рамках классической физики термоэлектронную эмиссию можно описать законом Больцмана, приняв за no плотность электронов внутри металла, n' плотность электронов в электронном облаке. При этом потенциальная энергия электронов внутри металла, соединенного с землей, определится уравнением
 .
.
Потенциальная же энергия электронов в электронном облаке
 ,
,
где j' – потенциал поля, образуемого зарядом электронного облака.
Разность между этими потенциальными энергиями
 .
.
Поэтому формула Больцмана для электронного облака, находящегося в равновесии с металлом, запишется так:
 . (7.5)
. (7.5)
Потенциал j' является функцией координат. Следовательно, плотность электронов вне металла будет также функцией координат. Так как в общем случае j>0, а j'<0, то наибольшая плотность электронного облака будет у поверхности металла (j'= 0):
 . (7.6)
. (7.6)
Из формулы (7.6) видно, что для усиления термоэлектронной эмиссии необходимо повысить температуру металла или взять металл с меньшей работой выхода.
С точки зрения современных представлений, явление термоэлектронной эмиссии можно объяснить так. В металле имеется электронный газ. В условиях термодинамического равновесия распределение электронов по энергетическим уровням определяется статистикой Ферми-Дирака:
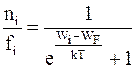 , (7.7)
, (7.7)
где ni – число электронов, имеющих энергию Ei;
fi – число квантовых состояний, соответствующих энергии Ei;
WF – энергия Ферми при температуре T, которая при T®0 K стремится к энергии Ферми WFo.
При этом
 .
.
Принимая во внимание, что во всех практически интересных случаях WF>>k×T, можно в формуле (7.7) величину WF считать равной WFо.
Если энергия покоящегося электрона вблизи поверхности – вне металла Wo, то формула (7.7) позволяет вычислить вероятность того, что электрон имеет энергию Wo. Эта вероятность не равна нулю и тем больше, чем выше температура. Таким образом, вблизи поверхности металла имеется электронное облако, которое находится в равновесии с электронным газом внутри металла. Это равновесие динамическое: электроны внутри металла, обладающие достаточно большей кинетической энергией, преодолевая силы, удерживающие их внутри металла, выходят за его пределы. Электроны вблизи металла при соответствующих направлениях их скоростей и местоположения захватываются силами, удерживающими электроны внутри металла. Таким образом, в условиях динамического равновесия сквозь поверхность металла протекают противоположно направленные токи, силы которых равны по модулю. Суммарная сила тока сквозь поверхность равна нулю.
Электроны с кинетической энергией Wk вблизи поверхности металла имеют полную энергию Wi = Wк + Eo и формула (7.7) принимает следующий вид:
 , (7.8)
, (7.8)
где Ф = (Wo - WF) – работа выхода электронов из металла.
Из формулы (7.8) видно, что плотность электронного облака вблизи поверхности металла сильно зависит от работы выхода и резко уменьшается с ее увеличением.
 Если вблизи поверхности металла существует электрическое поле, то электроны облака приходят в движение, и образуется электрический ток, называемый термоэлектронным. Очевидно, что сила тока должна расти с увеличением разности потенциалов.
Если вблизи поверхности металла существует электрическое поле, то электроны облака приходят в движение, и образуется электрический ток, называемый термоэлектронным. Очевидно, что сила тока должна расти с увеличением разности потенциалов.
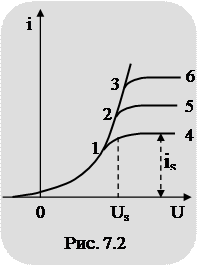
Зависимость силы тока между двумя электродами (анодом и катодом в вакуумном диоде) от разности потенциалов (анодного напряжения) представлена на рис. 7.2 (кривая 014).
Когда потенциал анода равен нулю, сила тока через диод мала. При увеличении положительного потенциала анода сила тока возрастает в соответствии с кривой 01. При дальнейшем возрастании анодного напряжения сила тока достигает некоторого максимального значения is, называемого током насыщения, и почти перестает зависеть от анодного напряжения (участок характеристики 14).
При увеличении температуры катода характеристика отображается кривыми 0125, 01236 и т.д.
При значениях тока, меньших is, зависимость силы тока от напряжения при всех температурах изображается одной и той же кривой 0123.
 Различными при разных температурах оказываются значения тока насыщения is, которые быстро увеличиваются при возрастании температуры катода. При этом увеличивается то анодное напряжение Us, при котором устанавливается ток насыщения.
Различными при разных температурах оказываются значения тока насыщения is, которые быстро увеличиваются при возрастании температуры катода. При этом увеличивается то анодное напряжение Us, при котором устанавливается ток насыщения.
Такая зависимость термоэлектронного тока от напряжения объясняется следующим образом. При термоэлектронной эмиссии в пространстве между катодом и анодом в любой момент времени находятся электроны, движущиеся от катода к аноду. Они образуют электронное облако отрицательного заряда (пространственный заряд). Этот пространственный заряд изменяет распределение потенциала между анодом и катодом. Если катод и анод представляют собой плоские пластины, параллельные друг другу, то в отсутствие пространственного заряда (при холодном катоде) распределение потенциала между катодом и анодом, образующими плоский конденсатор, изображается прямой линией 1 (рис. 7.3). При наличии термоэлектронного тока (нагревание катода) между катодом и анодом возникает пространственный заряд, и распределение потенциала изменяется (кривая 2). При этом значение потенциала в любой плоскости, находящейся на расстоянии x от катода, оказывается меньше, чем в отсутствие пространственного заряда. Следовательно, скорости движения электронов при наличии пространственного заряда уменьшаются. С увеличением анодного напряжения концентрация электронов в электронном облаке уменьшается. Поэтому и тормозящее действие пространственного заряда делается меньше, и анодный ток увеличивается.
Надо отметить, что такое распределение потенциала, изображенное кривой 2, имеет место тогда, когда начальные скорости вылета электронов из катода достаточно малы. В тех случаях, когда начальными скоростями нельзя пренебречь, распределение потенциала имеет более сложный вид.
Плотность тока насыщения определяется соотношением
 или
или  , (7.9)
, (7.9)
где C =  =
=  – универсальная постоянная, одинаковая для всех металлов;
– универсальная постоянная, одинаковая для всех металлов;
А – работа выхода электронов из катода.
Равенство (7.9) называется формулой Ричардсона-Дешмана. Для экспериментальной проверки эту формулу удобнее представить в виде
 . (7.10)
. (7.10)
Из формулы (7.36) можно сделать вывод, что зависимость lnjs от обратной величины абсолютной температуры катода на графике изображается прямой линией (рис. 7.4), угол наклона которой определяется соотношением

 . (7.11)
. (7.11)
Определяя экспериментально зависимость тока насыщения от температуры, можно определить работу выхода (ej) для данного металла.
Оказывается, что плотность тока в вакууме пропорциональна напряжению U в степени три вторых:
 , (7.12)
, (7.12)
где
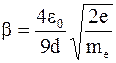 ;
;
U – напряжение (разность потенциалов) между катодом и анодом.
Уравнение (7.12) отображает закон трех вторых (закон Богуславского-Ленгмюра).
Закон трех вторых представлен в качестве примера нелинейного соотношения между силой тока и напряжением. Он не имеет универсального характера и даже в приведенном случае справедлив лишь в сравнительно узком интервале напряжений и токов. Нелинейность вольтамперной характеристики является наиболее важной особенностью многих элементов радио - и электротехнических схем, включая элементы твердотельной электроники.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 134; Нарушение авторских прав?; Мы поможем в написании вашей работы!