Решение минимаксных (максиминных) задач о назначениях

Решить задачи о назначениях алгоритмом Куна.

Задача 4.1.

J(i)/R(i)	R 1	R 2	R 3	R 4	R 5
J 1
J 2
J 3
J 4
J 5

Задача 4.2.

J(i)/R(i)	R 1	R 2	R 3	R 4	R 5
J 1
J 2
J 3
J 4
J 5

Задача 4.3.

J(i)/R(i)	R 1	R 2	R 3	R 4	R 5
J 1
J 2
J 3
J 4
J 5

Задача 4.4.

J(i)/R(i)	R 1	R 2	R 3	R 4	R 5
J 1
J 2
J 3
J 4
J 5

Задача 4.5.

J(i)/R(i)	R 1	R 2	R 3	R 4	R 5
J 1
J 2
J 3
J 4
J 5

Задача 4.6.

J(i)/R(i)	R 1	R 2	R 3	R 4	R 5
J 1
J 2
J 3
J 4
J 5

Задача 4.7.

J(i)/R(i)	R 1	R 2	R 3	R 4	R 5
J 1
J 2
J 3
J 4
J 5

Задача 4.8.

J(i)/R(i)	R 1	R 2	R 3	R 4	R 5
J 1
J 2
J 3
J 4
J 5

Задача 4.9.

J(i)/R(i)	R 1	R 2	R 3	R 4	R 5
J 1
J 2
J 3
J 4
J 5

Задача 4.10.

J(i)/R(i)	R 1	R 2	R 3	R 4	R 5
J 1
J 2
J 3
J 4
J 5

Рассмотрим задачу о назначениях с матрицей производительностей

R= 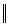r(i,j) 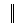(5x5), элемент которой r(i,j) - время выполнения работы с номером i исполнителем с номером:

J(i)/R(i)	R(1)	R(2)	R(3)	R(4)	R(5)
J(1)
J(2)
J(3)
J(4)
J(5)

Через X= 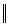x(i,j) 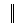- обозначим (5x5) матрицу, элементы которой x(i,j) {0,1}, причем, если x(i,j) = 1, то работа с номером i будет закреплена за исполнителем с номером j, если x(i,j) =0, то работа с номером i не будет закреплена за исполнителем с номером j.

Требуется так назначить исполнителей по работам, чтобы выполнялись условия канонической задачи о назначениях (каждый исполнитель назначается точно на одну работу, а каждая работа получает точно одного исполнителя) и минимальная из производительностей (от найденного назначения) была бы максимальна.

Для решения задачи применим алгоритм, основанный на последовательном решении ряда простейших задач о назначениях.

Обозначим через m=min r(i,j), где минимум берется по всем i, i=1,2,3,4,5, j=1,2,3,4,5. Тогда m=1.

Через M= min{min(max r(i,j)), min(max r(i,j))}, где max берется в первом члене по i, i=1,2,3,4,5, а во втором члене по j=1,2,3,4,5. Соответственно, max берется (в скобках) сначала по j, j=1,2,3,4,5, а затем по i, i=1,2,3,4,5.

M=min{ min(5,7,5,7,5), min(5,7,5,6,7)}=5.

Пусть m’ [1, 5].

Для осуществления двоичного поиска, положим m’=3.

Рассмотрим простейшую задачу о назначениях с матрицей R’, элемент которой r(i,j) = 0, если r(i,j) 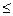3; r(i,j) = 1, если r(i,j) > 3.

Получим простейшую задачу о назначениях с матрицей Q:

J(i)/R(i)	R(1)	R(2)	R(3)	R(4)	R(5)
J(1)
J(2)
J(3)
J(4)
J(5)

Эта задача имеет решение (решать ее можно, например, используя алгоритм Форда-Фалкерсона поиска максимального потока в транспортной сети).

x’(1,2)=1, x’(2,4)=1, x’(3,3)=1, x’(4,1)=1, x’(5,5)=1.

Отсюда, исходная задача допускает решение со значением оптимума не меньше чем m’=4.

Попытаемся получить лучшее решение. Для этого выберем в качестве m’=4 и построим новую матрицу простейшей задачи о назначениях Q’:

J(i)/R(i)	R(1)	R(2)	R(3)	R(4)	R(5)
J(1)
J(2)
J(3)
J(4)
J(5)

Эта задача не имеет решения (например, из-за того, что исполнители J(1) и J(3) могу выполнять (по матрице Q’) лишь одну работу R(3).

Таким образом, оптимальное назначение определяется случаем, когда m’=3 и задается следующими значениями матрицы неизвестных:

x’(1,2)=1, x’(2,4)=1, x’(3,3)=1, x’(4,1)=1, x’(5,5)=1, остальные переменные равны нулю.

Дата добавления: 2017-02-01