Частные решения уравнения диффузии

Из общих решений уравнения диффузии при D = const, приведённых в 5.3, могут быть получены частные решения для различных начальных и граничных условий.

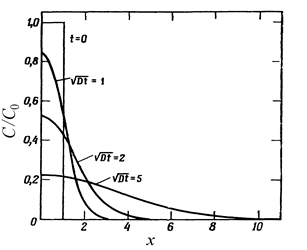
1. Диффузия с постоянной поверхностной концентрацией (из неогра-ниченного источника). При постоянной концентрации на поверхностности в течение всего процесса диффузии (С (0, t) = C _s = const) и первоначальном отсутствии примеси в образце (C (x, 0) = 0) профиль распределения примеси выражается дополнительной функцией ошибок (рис. 5.4)

.

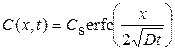Количество примеси, продиффундировавшее в образец,

.

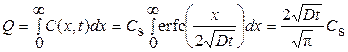Описанные условия соответствуют первой стадии диффузии.

2. Диффузия из слоя конечной толщины. Исходная примесь первоначально находится в слое толщиной h, т. е. C (x, 0) = C ₀ при x ≤ h и

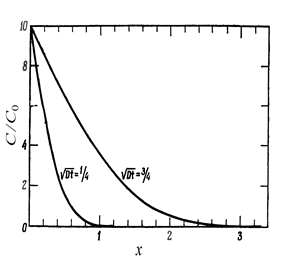
C (x, 0) = 0 при x > h, испарение с поверхности отсутствует (отражающая граница), 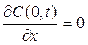. В этом случае решение уравнения диффузии имеет вид (рис. 5.5)

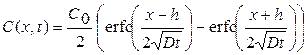
3. Диффузия из бесконечно тонкого слоя (из ограниченного источника).

Для бесконечно тонкого слоя при h → 0 из последнего выражения с учётом соотношения 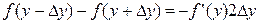получаем

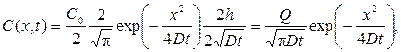
где Q – количество примеси в слое, Q = C ₀ h.

4. Двухстадийная диффузия. Если эффективная толщина диффузион-ного слоя, сформированного на первой стадии h ₁ = , значительно меньше толщины диффузионного слоя, сформированного на второй стадии h ₂ = 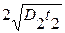, или D ₁ t ₁ << D ₂ t ₂, тогда можно использовать выражение, полученное ранее для бесконечно тонкого слоя,

,

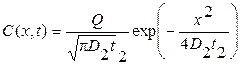где Q – количество примеси в слое, введённое во время первой стадии,

.

Здесь индекс 1 указывает на первую стадию, а индекс 2 – на вторую.

5. Многоэтапная диффузия. Под многоэтапной диффузией понимается диффузия в несколько этапов, на которых граничные условия не изменяются. В этом случае вид выражений для распределения примеси не изменяется, а произведение Dt заменяется на 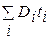, где i – номер этапа; t_i – длительность i -го этапа. Например, при двухэтапной диффузии из постоянного источника, когда концентрация на поверхности не меняется, С ₁(0, t) = С ₂(0, t) = C _s = = const,

.

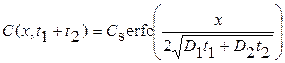При двухэтапной диффузии из ограниченного источника, когда граница при x = 0 непроницаема 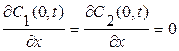и количество примеси в слое не меняется, Q ₁ = Q ₂ = Q = const,

.

Дата добавления: 2017-02-01