Расчет частотных характеристик механических и акустических звеньев с сосредоточенными и распределенными параметрами

Для построения частотной характеристики колебательного звена второго порядка необходимо и достаточно знать собственную частоту ω₀ (или соответствующий ей период Т₀) и коэффициент, характеризующий потери энергии в системе. В практических расчетах измерительных преобразователей потери энергии обычно характеризуются степенью успокоения р или добротностью Q. Однако встречаются и другие показатели потерь: d — затухание контура, δ — декремент затухающих колебаний, h — коэффициент затухания, с^-1. Все перечисленные показатели однозначно связаны между собой, и их соотношения имеют вид

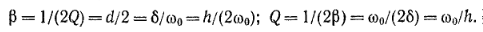
Значения Q или p, как правило, не поддаются точному расчету, однако они сохраняются постоянными для однотипных систем и поэтому могут быть установлены заранее на основе предыдущего опыта. Так, известно, что добротность электрических LС-контуров на низких звуковых частотах (50—500 Гц) составляет 10, а для высокочастотных контуров (на радиочастотах) не превосходит 200.

Внутреннее трение в металлах ограничивает степень успокоения механических резонансных систем (не имеющих специальных успокоителей) обычно значениями β= 0,06÷0,04, а их добротность, следовательно, составляет Q = 8÷12.

Рис.2.3.1

Значения собственной частоты механических систем, наоборот, могут быть весьма разнообразны (например, отдачей герца до 50 кГц) и поэтому всегда должны рассчитываться. Основными формулами для расчета собственной частоты при поступательном движении являются

а при вращательном движении

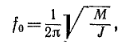
где m — масса системы, кг; W — жесткость, Н/м; n — податливость,
м/Н; М — удельный устанавливающий момент, Н·м (на 1 радиан);
J — момент инерции, кг· м².

Момент инерции J для конструкций, совершающих крутильные колебания и представленных на рис. 2-5, а, б, в, определяется следующими соотношениями: Вопросы расчета податливостей и жесткостей упругих элементов различных видов подробно рассмотрены ниже, в главе четвертой.

Расчет собственной частоты звена с сосредоточенными параметрами
покажем на примере расчета собственной частоты акселерометра с тензорезисторами (рис. 2.3.1 а). Представляя упругий элемент акселерометра как балку длиной l, шириной b и толщиной h, определим ее податливость как собственную частоту как

Однако подобный расчет является весьма приближенным. Фактором, который может вызвать отклонение частотной характеристики датчика от рассчитанной, является неучтенная податливость в месте заделки неподвижного конца упругого элемента в основание. Если изобразить механическую схему датчика с учетом этой податливости п _д, как это показано на рис. 2.3.1, б, то становится ясно, что податливости п и п _л суммируются и собственная частота оказывается ниже рассчитанной. Вторым фактором, вызывающим отклонение собственной частоты от рассчитанной, является то обстоятельство, что в любой реальной конструкции упругий элемент и закрепленная на нем масса имеют конечные размеры. Рассматривая систему с сосредоточенными параметрами, предполагаем, что упругий элемент — балка—имеет пренебрежимо малую массу по сравнению с массой т, а масса т имеет пренебрежимо малые размеры по сравнению с размерами балки, т. е. является материальной точкой.

Отступление от этих условий приводит к весьма существенному изменению частотной характеристики, так как в системе появляются резонансы на двух частотах (рис. 2.3.1, в) и частота первого из них оказывается ниже рассчитанной выше. В частности, если инерционную массу представить в виде цилиндра радиусом ,
где l — длина балки, то частота ω_1р = 0,73ω₀, а ω_2р = 2,7ω₀.

Рис.2.3.2

Собственная частота столба газа, заключенного в трубе с жесткими стенками и представляющего собой резонатор с равномерно распределенной по длине l массой и жесткостью, определяется скоростью распространения возмущения, т. е. скоростью звука в среде, заполняющей резонатор, и длиной последнего.

Скорость звука в газе определяется соотношением

где R —универсальная газовая постоянная, равная 8,314 Дж/(моль- К);
Θ— абсолютная температура, К; γ=c_p/c_v — отношение теплоемкостей при постоянном давлении и постоянном объеме; М — молекулярная масса газа; Р — давление газа, Па; ρ — плотность газа, кг/м³.

Акустический резонанс наступает на такой частоте, при которой звуковая волна за период Т₀ успевает пройти длину l в одном направлении, отразиться от противоположной стенки и пройти длину l в обратном направлении. При распространении волны со скоростью с на это требуется время Т₀ = 2 l/c. Отсюда собственная частота такого резонатора

Рис.2.3.3

Собственная частота продольных колебаний стержня, подвешенного
теоретически в пространстве за центр тяжести или столба жидкости
в трубчатом резонаторе как системы с равномерно распределенными по длине параметрами определяется аналогичным образом и равна f ₀ = с/(2 l), где с – скорость звука в стержне или жидкости; l — длина стержня или столба жидкости.

Собственная частота стержня, заделанного одним концом в тело с бесконечно большой массой, например пьезоэлектрического акселерометра, схематически представленного на рис.2.3.3, а, находится аналогично. Для приведения этой задачи к предыдущей реальной, заделанный одним концом стержень длиной l мысленно дополним его зеркальным изображением, как это показано на рис.2.3.3,б. Для такого закрепленного в центре тяжести стержня длиной 2 l собственная частота в соответствии с приведенной выше формулой равна f ₀ = с/(4 l).

Приближенный расчет сложных колебательных систем удобно производить путем замены их отдельных элементов с распределенными параметрами эквивалентными им по значению собственной частоты элементами с сосредоточенными параметрами. Покажем возможность такой
замены на примере заделанного стержня.

Скорость звука в твердом теле , где Е — модуль упругости материала тела, Н/м²; ρ — плотность материала, кг/м³. Отсюда для свободно подвешенного стержня длиной l

а для стержня, заделанного одним концом в тело с бесконечной массой,

Полная масса такого стержня длиной l площадью S и плотностью материала ρ равна m = S l ρ. Изменение δ его длины l под действием силы F равно δ = l σ/E = l F/(SE). Отсюда полная податливость стержня п = σ/F = l /(SE). Поэтому собственная частота системы, которая имела бы массу m, равную массе заделанного стержня, и податливость n, также равную податливости этого стержня, была бы равна

Отсюда действительное значение собственной частоты заделанного
стержня может быть выражено через его полные массу m и податливость п как

Различие частот f ₀ и f ' ₀обусловлено тем, что нижний торец стержня
(рис. 2-7) не совершает колебаний и поэтому в колебаниях участвует не вся масса стержня, а лишь некоторая ее часть. Отсюда произведение 0,4 т, входящее в формулу для f ₀, можно трактовать как некоторую эквивалентную массу т _экв = 0,4 т, используя значение которой, собственную частоту стержня можно определить по обычной формуле

Аналогично этому можно говорить и об эквивалентной податливости n _экв = 0,4 п, ибо верхний конец стержня (рис.2.3.3, а) не испытывает при колебаниях сжатия и растяжения, в которых участвует лишь нижняя часть стержня. С использованием значения n _экв собственная частота равна

Поэтому в общем виде можно считать, что собственная частота всегда может быть найдена как

но в первом случае т _экв = 0,4 т, а n _экв = п, а во втором т _экв = т, а n _экв = 0,4 п.

Подобные эквивалентные параметры могут быть найдены и для других колебательных систем. Например, для мембраны на рис.2.3.3, а, заделанной по контуру (если в качестве п _экв принять податливость ее центра),

т _экв=0,32 т. Для балки, лежащей на двух шарнирных опорах, т _экв = 0,485 т, а при заделанных концах т _экв = 0,371 т при расчете их податливости для центра балки. Для консольной балки постоянного сечения т _экв = 0,236 т, а для балки равного сопротивления т _экв = 0,067 т при использовании в расчете податливости свободного конца балки. Для натянутой ленты (см.

рис.2.3.3, в) при использовании податливости от силы по ее центру, как и для стержня, т _экв = (4/π²) т = 0,405 т.

Рис.2.3.4

Такая эквивалентная замена позволяет достаточно просто получить расчетные формулы для собственной частоты разнообразных и достаточно сложных конструкций преобразователей. Так, например, преобразователь пьезоэлектрического акселерометра (рис. 2.3.4, б) состоит из инерционной массы 1,пластин пьезокерамики 2 и основания 5, соединенных между собой клеем или пайкой. Благодаря тому, что модуль упругости керамики близок к модулю металлов, детали 1 и 2 можно рассматривать как единый стержень длиной l с эквивалентной массой, равной массе стержня т _ст, и эквивалентной податливостью, равной 0,4 податливости всего стержня п _ст. Основание 3 можно рассматривать как мембрану, заделанную по кон-
туру и нагруженную в центре
массой стержня.

Так как в колебаниях всей системы масса стержня участвует полностью, а масса мембраны — лишь частично, то эквивалентная масса всей системы т _экв = т _ст +0,32 m _осн. Податливость же мембраны, наоборот, используется
полностью, в то время как податливость стержня участвует лишь частично. Поэтому эквивалентная податливость системы n _экв = п _осн +0,4 п _ст. Отсюда собственная частота всей системы равна

Дата добавления: 2017-02-01