
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Эквивалентные электрические схемы механо-электрических преобразователей
|
|
|
|
В измерительной технике часто используются такие преобразователи, частотные характеристики которых определяются частично электрическими, а частично механическими (или акустическими) параметрами. В подобных случаях удобнее все параметры привести к какому-то единому (лучше электрическому) виду и весь преобразователь изобразить в виде некоторой эквивалентной (т. е. обладающей теми же частотными свойствами) электрической цепи, которая отразила бы как электрические, так и механические элементы. Это может быть достигнуто методом, который получил название метода эквивалентных схем или электрических схем замещения и основывается на общности дифференциальных уравнений электрических и механических систем.
На рис. 2-9 показаны механическая колебательная система и ее электрический аналог в виде последовательного и параллельного контуров.
Дифференциальное уравнение механической системы может быть
записано в виде
или в виде
 (2.4.1)
(2.4.1)
или в виде
 (2.4.2)
(2.4.2)
где F — приложенная сила; т — масса подвижной части; Р — коэффициент успокоения, характеризующий вязкое трение; п — податливость пружины; х — перемещение подвижной части; v = dx/dt — скорость движения подвижной части.

Рис.2.4.1
Дифференциальное уравнение последовательного контура может
быть записано в виде
 (2.4.3)
(2.4.3)
Дифференциальное уравнение параллельного контура
 (2.4.4)
(2.4.4)
Сравнение дифференциальных уравнений (2.4.1), (2.4.3) и (2.4.2), (2.4.4)
показывает, что механическая система может быть заменена как последовательным, так и параллельным электрическим контуром. В табл. 2.4.1 представлены электрические аналоги механических параметров для того и другого контура.
Таблица 2.4.1
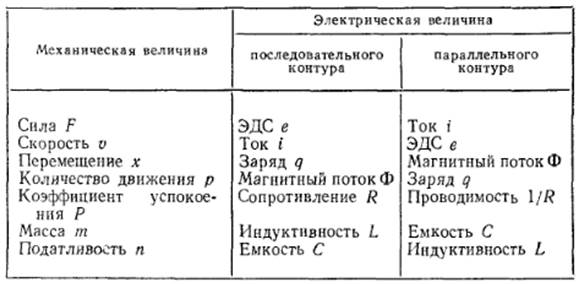
Метод электромеханических аналогий широко применяется при расчете измерительных преобразователей (см., например, работу [2]). Для сопоставления эквивалентной схемы нужно выбрать электрический аналог механической системы и определить коэффициент электромеханической связи k эм, равный k эм= F/ v = –i/ v для последовательной схемы электрического аналога и k эм = F/i = – U/ v для параллельной схемы. Элемент связи между реальной электрической цепью и электрическим аналогом механической системы представляет собой идеальный трансформатор с коэффициентом трансформации, равным k эм. Особенностью трансформатора является то, что его коэффициент трансформации измеряется в ньютонах на вольт или на ампер. Приведя все сопротивления и проводимости к первичной обмотке трансформатора, можно составить окончательную эквивалентную схему – электрическую схему замещения, которая отражает действительные свойства системы со стороны электрических зажимов.
Сущность метода эквивалентных схем, или электрических схем замещения, рассмотрим на примере преобразователей с электромаг нитной и электростатической связью механической и электрической
систем, наиболее распространенных в измерительной технике.

Рис.2.4.2
Эквивалентные схемы электромеханических преобразователей с электромагнитной связью. Примерами таких преобразователей могут служить магнитоэлектрический преобразователь тока I в силу F, схематически показанный на рис. 2-10, а, или магнитоэлектрический измерительный механизм. Механическая система преобразователя обладает массой т, подвешенной на пружине с жесткостью W, и имеет успокоение Р, обусловленное внутренним трением в элементах подвески и сопротивлением воздуха движению катушки в зазоре магнита. Электрическая система обладает сопротивлением R0 и индуктивностью L0 катушки преобразователя.
При измерении сопротивления такого преобразователя на постоянном токе обнаруживаем лишь сопротивление R0 его катушки. При повышении частоты питающего тока можно было бы ожидать повышения сопротивления по штриховой кривой на рис. 2-10, б, соответствующей

Однако фактически наблюдаем повышение сопротивления преобразователя в виде резонансного пика на частоте f р, соответствующей резонансу механической системы преобразователя и близкой к

Физически это явление объясняется так. В области механического
резонанса резко нарастает амплитуда механических колебаний катушки в зазоре постоянного магнита, наводимая в катушке ЭДС направлена встречно внешнему возбуждающему напряжению, вычитается из него, и ток, проходящий через преобразователь, падает, что формально мы и воспринимаем как возрастание ZΣ преобразователя. Это возрастание ZΣ преобразователя можно представить как появление некоторого дополнительного электрического сопротивления Zвн, вносимого механической системой и называемого вносимым сопротивлением.
Для установления вида связи электрических и механических параметров преобразователя уточним, как возникают механическая сила и встречная ЭДС в катушке преобразователя. Как известно, механическая сила F, возникающая от протекания по катушке тока i, равна F = i B l = k эм i, где В — индукция в зазоре магнита; l — длина проводника катушки; k эм = В l — так называемый коэффициент электромагнитной связи.
ЭДС, наводимая в катушке при ее движении в магнитном поле постоянного магнита, равна е = – d Ф/ d t = – v B l = – k эм v, где k эм = B l — тот же коэффициент электромагнитной связи, а v — скорость движения катушки.
Для составления полной системы уравнении обозначим R0 + j(ωL =
= Z0, а отношение механической силы F к механической скорости v назовем комплексным механическим сопротивлением Zмх = F/ v. Тогда полная система уравнений, описывающая преобразователь, будет

ибо напряжение u на зажимах преобразователя складывается из падения напряжения от тока i на элементе Z0 и ЭДС е =– k эм v наводимой в катушке, а сила, развиваемая катушкой, — из силы Zмх v, обусловленной ее движением, и силы k эм i, создаваемой током.
Если внешняя сила F, развиваемая катушкой, равна нулю (преобразователь не нагружен на внешние устройства), то из второго уравнения следует, что

Полное электрическое сопротивление преобразователя

а после подстановки значения v

т. е. складывается обычным образом из электрическою Z0 и вносимого
Zвн = k2 эм/Zмх сопротивлений преобразователя.
Особенностью связи Zвн и Zмх является их обратная пропорциональность друг другу: чем больше Zмх, тем меньше Zвн. В этом легко убедиться, сделав Zмх = ∞, т. е. застопорив катушку, лишив ее возможности двигаться. При этом будет ZΣ = Z0, Zвн = 0, т. е. влияние механических параметров на ZΣ исчезнет.
Для того чтобы уяснить, из каких электрических элементов может
быть смоделировано в электрической цепи вносимое сопротивление Zвн,
обусловленное влиянием механических элементов преобразователя, воспользуемся вместо жесткости обратной ей величиной — податливостью п= 1/W и представим механическое сопротивление Zмх в виде

Тогда

т. е. результирующая проводимость Yвн = 1/ Zвн складывается из параллельно соединенных трех проводимостей, первая из которых не зависит от текущего значения частоты со и, следовательно, может быть смоделирована как

вторая пропорциональна частоте ω, т. е. в электрической цепи должна
быть представлена емкостью с проводимостью

а третья, обратно пропорциональная частоте, может быть смоделирована индуктивностью с проводимостью

Таким образом, результирующая эквивалентная схема преобразователя с массой т, податливостью п и активным механическим сопротивлением r мх для воспроизведения частотной характеристики, показанной на
рис. 2-10, б, должна состоять из элементов, изображенных на рис. 2-10, в или 2-10, г, где R1 = k2 эм/ r мх; С1 = m/ k2 эм; L1= k2 эм n = k2 эм/W.
В результате выбранный путь приводит к эквивалентной параллельной схеме и коэффициенту k эм = F/i = Вl.
В том, что полученная эквивалентная схема (рис. 2-10, г) действительно соответствует фактической частотной характеристике преобразователя, приведенной на рис. 2-10, б, легко убедиться, просматривая характерные точки этой характеристики. В самом деле, при ω= 0 сопротивления катушек L0 и L1 равны нулю и ZΣ= R0. Резонансный пик характеристики (если пренебречь влиянием L0) определяется резонансом контура C1Ll и рассматривается вблизи собственной частоты

а при дальнейшем повышении частоты сопротивление конденсатора C1
стремится к нулю и ZΣ = R0 + j ωL0.
Поляризованный электромагнитный преобразователь (рис. 2.4.3)
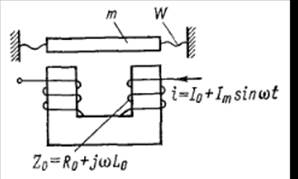
Рис.2.4.3
Постоянное подмагничивание создается током I0 и МДС подмагничивания Fм =I0ω или постоянным магнитом, имеющим МДС Fм = Н l м
где Н — напряженность и l м— длина магнита. Поскольку электромагнитная сила определяется током то, как и в предыдущем примере удобнее выбрать параллельную эквивалентную схему. Электромагнитная сила Fэм=  , где
, где
δ– длина зазора; S — площадь зазора;
μ0–магнитная проницаемость и i = I0+I т sin ωt – ток через преобразователь.
Составляющая силы, имеющая частоту ω, определяется как
 .
.
Отсюда находим коэффициент электромеханической связи

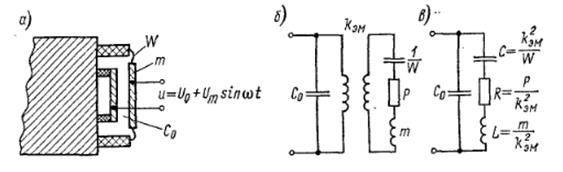
Рис.2.4.5
если этот коэффициент выразить через подмагничивающий поток
Ф0=  , то k эм= Ф0ω/δ. Эквивалентная схема остается той же, что и представленная на рис. 2.4.2, г.
, то k эм= Ф0ω/δ. Эквивалентная схема остается той же, что и представленная на рис. 2.4.2, г.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 95; Нарушение авторских прав?; Мы поможем в написании вашей работы!