Самостоятельная работа обучающего характера.

II. Выполнение работы по вариантам.

Вариант I

1. На рисунке 1 отрезки АВ и СD имеют общую середину О. Докажите, что DАО = СВО.

2. Луч АD – биссектриса угла А. На сторонах угла А отмечены точки В и С так, что АDВ = АDС. Докажите, что АВ = АС.

3. Начертите равнобедренный треугольник АВС с основанием ВС. С помощью циркуля и линейки проведите медиану ВВ ₁ к боковой стороне АС.

Вариант II

1. На рисунке 2 отрезки МЕ и РK точкой D делятся пополам. Докажите, что KМD = РЕD.

2. На сторонах угла Д отмечены точки М и K так, что DМ = DK. Точка Р лежит внутри угла D и РK = РМ. Докажите, что луч DР – биссектриса угла МDK.

3. Начертите равнобедренный треугольник АВС с основанием АС и острым углом В. С помощью циркуля и линейки проведите высоту из вершины угла А.

Вариант III
(для более подготовленных учащихся)

1. На рисунке 3 прямые АВ и СD пересекаются в точке Е, СЕ = ВЕ, С = В; АА ₁ и DD ₁ – биссектрисы треугольников АСЕ и DВЕ. Докажите, что АА ₁ = DD ₁.

2. На сторонах угла А отмечены точки В и С так, что АВ = АС. Точка М лежит внутри угла А и МВ = МС. На прямой АМ отмечена точка D так, что точка М лежит между точками А и D. Докажите, что ВМD =
= СМD.

3. Начертите равнобедренный тупоугольный треугольник АВС с основанием ВС и с тупым углом А. С помощью циркуля и линейки проведите:

а) высоту треугольника АВС из вершины угла В;

б) медиану треугольника АВС к стороне АВ;

в) биссектрису треугольника АВС угла А.

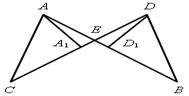
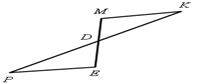
Рис. 1 Рис. 2 Рис.3

Урок 3
признаки параллельности двух прямых

1. повторить материал пунктов 2–21.

1) По рисунку 1 назовите пары накрест лежащих, односторонних, соответственных углов.

2) На рисунке 2 4 = 6.

Докажите, что 5 = 3; 8 = 6; 2 = 5.

3) На рисунке 3 1 = 5:

а) выпишите все пары накрест лежащих углов и докажите, что в каждой паре углы равны;

б) выпишите все пары соответственных углов и докажите, что в каждой паре углы равны;

в) выпишите все пары односторонних углов и докажите, что сумма углов в каждой паре равна 180°.

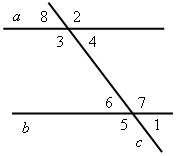
Рис. 1 Рис. 2 Рис. 3

2.. Повторить признаки равенства треугольников и утверждение о том, что две прямые, перпендикулярные к третьей, не пересекаются (п. 12).

1. Задача. Найти пары параллельных прямых (отрезков) и доказать их параллельность (по готовым чертежам на доске (см. рис. 1–3):

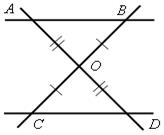
Рис. 1 Рис. 2 Рис. 3

3.. Решить задачу № 191 на доске и в тетрадях учащихся.

Рис. 4

Дано: АВС; ВK – биссектриса. ВМ = МK. Докажите, что KМ | | АВ.

Доказательство

По условию ВМ = МK, тогда треугольник ВМK – равнобедренный (по определению), значит, МВK = МKВ (углы при основании равнобедренного треугольника равны). По условию ВK – биссектриса В, то МВK = АВK.

Следовательно, АВK = МВK = МKВ, а АВK и МKВ – накрест лежащие углы, тогда АВ | | KМ.

4. Задание: найти пары параллельных прямых (отрезков) и доказать их параллельность.

Рис. 1 Рис. 2 Рис. 3

5. Решить задачи по готовым чертежам на заготовленных плакатах (см. рис. 4–6):

Рис. 4 Рис. 5 Рис. 6

Найдите пары параллельных прямых и докажите их параллельность.

6. Решить задачу № 192 в тетрадях.

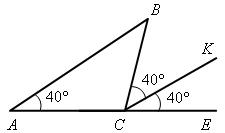Рис. 5

Дано: АВС; А = 40°; ВСЕ = 80°; СK – биссектриса ВСЕ. Доказать: СK || АВ.

Доказательство

ВСЕ = 80° по условию; СK – биссектриса ВСЕ, тогда ВСK =
= KСЕ = 80°: 2 = 40°. По условию А = 40° и получили KСЕ = 40°, а эти углы соответственные при прямых АВ и KС и секущей АЕ. Значит, АВ || СK по признаку параллельности прямых.

7. Решить задачи (по готовым чертежам (см. рис. 1–5)):

Рис. 1	Рис. 2	Рис. 3
Докажите, что а || b.	Докажите, что а || с.	Докажите, что а || b и m || n, если 1 = 2 = 3.
Рис. 4	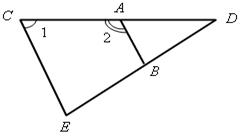Рис. 5
Дано: 1 = 83°; 2 больше 1 на 14°. Параллельны ли прямые MN и АВ?	Дано: 2 = 114°; 1 меньше 2 на 20°. Параллельны ли сторона СЕ и прямая АВ?

Вариант I

1. Параллельны ли прямые d и е, изображенные на рисунке 1?

2. На рисунке 2 точка О – середина отрезков EL и KF. Докажите, что EF || KL.

Вариант II

1. Параллельны ли прямые m и n, изображенные на рисунке 3?

2. На рисунке 4 отрезки MО и NP пересекаются в их середине F. Докажите, что MN || PO.

Рис. 1 Рис. 2

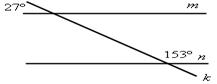
Рис. 3 Рис. 4

Вариант III

1. Какие из прямых m, n и p, изображенных на рисунке 5, являются параллельными? Ответ обоснуйте.

2. В равнобедренных треугольниках СDЕ и FPK, изображенных на рисунке 6, 1 = 2. Докажите, что СD || PF.

Вариант IV

1. На рисунке 7 МD = NP, 1 = 2. Докажите, что MN || DP.

2. В равнобедренных треугольниках АВС и DЕF, изображенных на рисунке 8, 1 = 2. Докажите, что AB || EF.

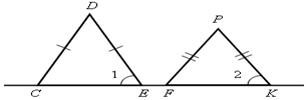
Рис. 5 Рис. 6

Рис. 7 Рис. 8

Дата добавления: 2017-02-01