Машина Поста

Дополнительное обследование

· Общеклинические анализы (ОАК, ОАМ)

· Определение группы крови и резус принадлежности

· Биохимический анализ крови (сахар крови, билирубин общий, прямой, непрямой, белок, мочевина)

· ЭКГ

· Рентгенография органов грудной клетки

Оперативное лечение:

-Накостный остеосинтез правой плечевой кости пластиной с шурупами.

Ежедневные перевязки послеоперационной раны.

Контрольная рентгенограмма правой плечевой кости.

Реабилитация:

1. ЛФК

2. Массаж

3. Физиотерапевтические процедуры

4. Клинические и функциональные пробы

Прогноз:

Прогноз для жизни и здоровья данной больной благоприятный, т.к. не было повреждения жизненно важных органов, при правильном выполнении реабилитационных мероприятий послеоперационных осложнений не будет.

Больной через 3-4 месяца будет трудоспособен.

Список использованной литературы:

1. Траматология и ортопедия: Учебник / Под ред. Проф.В.М. Шаповалова, проф. А.И.Грицанова, доц. А.Н. Ерохова. – Спб: ООО «Издательство Фолиант», 2004.

2. «Основы травматологии и ортопедии» А. А. Коломиец, Е. А. Распопова. Г. Барнаул 2002 год.

Машина Поста – розроблена у 1936 році математиком Емілєм Постом абстрактна машина, яка формально визначає алгоритм.

Машина Поста складається з необмеженої в обидва боки стрічки, розділеної на гнізда, послідовно пронумеровані цілими числами, як позитивними, так і негативними. У кожнім гнізді стрічки стоїть ознака того, що в гнізді записана мітка або гніздо порожнє. Стан стрічки — це дані, які гнізда зайняті, а які порожні.

Крім стрічки є головка читання/запису, яка уміє рухатися вперед, назад і стояти на місці; уміє читати вміст, стирати й записувати мітку; управляється програмою, у яку можуть входити в будь-якій комбінації й будь-якій кількості шість команд:

1. вправо;

2. уліво;

3. поставити мітку;

4. стерти мітку;

5. передача керування на один номер команди в програмі, якщо в поточнім гнізді є мітка; якщо мітки ні, те передача керування на інший номер команди;

6. припинення роботи.

1.4. Машина Т’юринга

Формальні визначення алгоритму з'явилися в тридцятих-сорокових роках 20 століття. Одним із перших було визначення англійського математика Алан Тюринга, який в 1936 році описав схему деякої гіпотетичної (абстрактної) машини і запропонував називати алгоритмами те, що вміє робити така машина. При цьому визначенні, якщо щось не може бути зроблено машиною Тюринга, це вже не алгоритм.

Інакше кажучи, Тюринг формалізував правила виконання дій за допомогою опису роботи деякої конструкції.

Маши́на Тю́ринга — математичне поняття, введене для формального уточнення інтуітивного поняття алгоритму. Названа на честь англійського математика Алана Тюринга, який і запропонував це поняття в 1936. Аналогічну конструкцію машини згодом і незалежно від Тюринга ввів американський математик Еміль Пост.

Формальні визначення алгоритму з'явилися в тридцятих-сорокових роках 20 століття. Одним із перших було визначення англійського математика Алан Тюринга, який в 1936 році описав схему деякої гіпотетичної (абстрактної) машини і запропонував називати алгоритмами те, що вміє робити така машина. При цьому визначенні, якщо щось не може бути зроблено машиною Тюринга, це вже не алгоритм. Інакше кажучи, Тюринг формалізував правила виконання дій за допомогою опису роботи деякої конструкції.

У кожної машини Тюринга є стрічка, потенційно нескінчена в обидві сторони. Є скінчена множина символів стрічки S₀, …, S_n, що називається алфавітом машини. У кожний момент часу кожна комірка може бути зайнята не більш ніж одним символом. Машина має деяку скінчену множину внутрішніх станів q₀, q₁, …, q_n. У кожний даний момент часу машина знаходиться в тільки одному із цих станів.

Нарешті, є голівка, яка у кожний даний момент часу знаходиться на одній із комірок стрічки. Машина діє не безупинно а лише в дискретні моменти часу. Якщо в якійсь момент t голівка сприймає комірку (тобто знаходиться на комірці), що містить символ S_i, і машина знаходиться у внутрішньому стані q_j, то дія машини визначена, і однією із чотирьох дій:

– голівка стирає символ S, і записує в тій же комірці новий символ S_k,

– голівка пересувається в сусідню ліву комірку,

– голівка пересувається в сусідню праву комірку,

– машина зупиняється.

У випадках (1)-(3) машина переходить у новий внутрішній стан q_r, і готова знову до дії в такий момент t + 1. Будемо припускати, що символ S₀ представляє порожню комірку, і отже, голівка завжди сприймає деякий символ.

Перші три з можливих дій машини можуть бути описані відповідно такими упорядкованими четвірками, які ми надалі будемо називати командами:

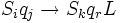
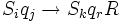
Тут перші два символа — це відповідно внутрішні стани машини і сприйнятий символ, наступні три визначають дію машини (запис голівкою символу S_k, або переміщення голівки на одну комірку вліво, або переміщення голівки на одну комірку вправо) та новий стан машини. Якщо стрічка вкладена в машину Тюринга, голівка машини встановлена на одну із комірок стрічки і машина приведена в один із своїх внутрішніх станів, то машина починає оперувати на стрічці: її голівка пише і стирає символи і пересувається з однієї комірки в іншу. Якщо при цьому машина колись зупиняється, то стрічка, яка знаходиться в ній в цей момент, називається результатом застосування машини до даної стрічки.

Незважаючи на свій простий устрій, машина Тюринга може виконувати складні перетворення слів. Спочатку, коли стрічка містить вхідне слово, автомат знаходиться проти деякої з комірок і у якомусь стані. У залежності від вибору початкової комірки, утворяться різні результати роботи машини Тюринга. У процесі своєї роботи машина Тюринга буде ніби перестрибувати з однієї комірки програми на іншу, відповідно до інформації на стрічці і вказівками в командах програми, поки не дійде до команди, яка переведе автомат у кінцевий стан.

Розглянемо приклад простої машини Т’юринга.

Допустимо, ми маємо унарну систему числення:

Для якої описана наступна машина Т’юринга:

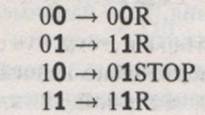
Пояснення: перша цифра (не виділена) зліва від стрілки означає стан, у якому машина знаходиться, а справа – стан, у який вона має перейти.

Виділена цифра зліва від стрілки – символ на стрічці, який в даний момент часу зчитує пристрій. Вона заміняє цей символ виділеною цифрою справа від стрілки.

R – означає, що пристрій має переміститися вздовж стрічки вправо, а L – вліво, STOP – зупинитися.

Навіщо потрібна дана машина?

Запустимо машину на наступній стрічці (початковий стан «0» і починає виконуватися з крайньої лівої позиції стрічки):

(Представлене на стрічці число представляє собою десяткове число «чотири»).

Розглянемо покрокове виконання машини:

– Машина зчитує «0», оскільки вона знаходиться у стані «0», то виконується наступна інструкція: 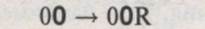, тобто машина записує на стрічку «0», переходить у стан «0» і переходить по стрічці вправо.

– …

– Машина зчитує «1», оскільки вона знаходиться у стані «0», то виконується наступна інструкція: 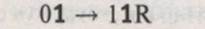, тобто машина записує на стрічку «1», переходить у стан «1» і переходить по стрічці вправо.

– Машина зчитує «1», оскільки вона знаходиться у стані «1», то виконується наступна інструкція: 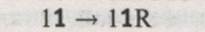, тобто машина записує на стрічку «1» переходить у стан «1» і переходить по стрічці вправо.

– …

– Машина зчитує «0», оскільки вона знаходиться у стані «1», то виконується наступна інструкція: 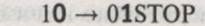, тобто машина записує на стрічку «1», переходить у стан «0» і зупиняється.

Який буде результат на стрічці?

Можливості машини Т’юринга

Описуючи різноманітні алгоритми для машин Т’юринга і стверджуючи реалізованість усіляких композицій алгоритмів, Т’юринг переконливо показав розмаїтість можливостей запропонованої їм конструкції, що дозволило йому виступити з такою тезою:

Всякий алгоритм може бути реалізований відповідною машиною Тюринга.

Це основна гіпотеза теорії алгоритмів у формі Т’юринга. Одночасно ця теза є формальним визначенням алгоритму. Завдяки їй можна доводити існування або неіснування алгоритмів, створюючи відповідні машини Т’юринга або доводячи неможливість їхньої побудови. Завдяки цьому з'являється загальний підхід до пошуку алгоритмічних рішень.

Якщо пошук рішення наштовхується на перешкоду, то можна використовувати цю перешкоду для доведення неможливості рішення, спираючись на основну гіпотезу теорії алгоритмів. Якщо ж при доказі неможливості виникає своя перешкода, то вона може допомогти просунутися в пошуку рішення, хоча б частково усунувши стару перешкоду. Так, по черзі намагаючись довести то існування, то відсутність рішення, можна поступово наблизитися до розуміння суті поставленної задачі.

Довести тезу Тюринга не можна, тому що в його формулюванні не визначене поняття всякий алгоритм, тобто ліва частина тотожністі. Його можна тільки обґрунтувати, представляючи різноманітні відомі алгоритми у вигляді машин Тюринга. Додаткове обґрунтування цієї тези складається в тому, що пізніше було запропоновано ще декілька загальних визначень поняття алгоритму і щораз вдавалося довести, що, хоча нові алгоритмічні схеми і виглядають інакше, вони в дійсності еквівалентні машинам Тюринга:

усе, що реалізовано в однієї з цих конструкцій, можна зробити й в інших

Ці твердження доводяться строго, тому що в них мова йде вже про тотожність формальних схем.

1.5. Основи лямбда-числення та функціонального програмування

Лямбда-числення – розділ дискретної математики, який вивчає обчислення як математичний процес. Лямбда-числення було винайдене на початку 1930-х років Алонзо Черчем.

В основу лямбда-числення покладено дві фундаментальні операції: аплікація та абстракція.

Аплікація – використання чи виклик функції по відношенню до певного значення. Позначається як f.a, де f – функція, а – деяке значення. Відповідає загально прийнятому у математиці запису f(a).

Абстракція – побудова функції по заданим виразам, за її допомогою можна конструювати нові функції.

Лямбда-числення послужило основою для функціонального програмування – парадигми програмування, яка розглядає програму як обчислення математичних функцій та уникає стани та змінні дані. Функціональне програмування наголошує на застосуванні функцій, на відміну від імперативного програмування, яке наголошує на змінах в стані та виконанні послідовностей команд.

Більш чітка концепція функціонального програмування визначає набір спільних правил та тем замість переліку відмінностей від інших парадигм. До таких, що часто вважаються важливими, належать функції вищого порядку та першого класу, замикання, та рекурсія.

Основну увагу функціональним мовам програмування, особливо, «чисто функціональним», приділи академічні дослідники. Однак, до відомих функціональних мов програмування, які використовуються в промисловості та комерційному програмуванні належить Erlang (паралельні програми), R (статистика), Mathematica (символьні обчислення)), J та K (фінансовий аналіз), та спеціалізовані мови програмування на кшталт XSLT. Істотний вплив на функціональне програмування здійснило лямбда числення, мова програмування APL, мова програмування Lisp та, новіша мова програмування Haskell.

В цілому функціональне програмування має декілька важливих переваг по відношенню до імперативного, зокрема:

— відсутність змінних означає, що стан програми зберігається в стеку викликів функцій та їх аргументах, завдяки чому помилки завжди локальні – зовнішні фактори на них не впливають;

— програми просто розпаралелювати у автоматичному режимі;

— для програм можна математично строго доводити їх правильність.

1.6. Теза Черча-Т’юринга про алгоритмічну розв’язність задачі

Теза Чорча-Тьюринга – фундаментальне твердження для багатьох областей науки, пов’язаних з інформатикою та програмуванням.

Теза Чорча-Тьюринга говорить наступне:

машина Тьюринга визначає те, що в математиці розуміють під алгоритмічною (механічною) процедурою. Таким чином, будь-який математичний алгоритм може бути реалізований за її допомогою.

1.7. Проблема розв’язності (зависання)

В теорії обчислювальності існує проблема зависання (обчислювальності): дано опис алгоритму та початкові вхідні дані, необхідно визначити, чи може алгоритм з цими вхідними даними завершитися коли-небудь. Альтернативою зупинки є ситуація, коли робота алгоритму не припиняється (він зависає).

Машина Т’юринга не може бути використана для вирішення проблеми зависання будь-якого алгоритму.

Тому подібна задача відноситься до алгоритмічно нерозв’язних задач

1.8. Алгоритмічно нерозв’язні задачі

Алгоритмічна нерозв’язність – важлива властивість деяких класів коректно поставлених задач, які допускають використання алгоритмів, яка полягає в тому, що задачі кожного із цих класів в принципі не мають якого-небудь загального універсального алгоритму вирішення, що об’єднує весь клас.

Незважаючи на повну однотипність умов та вимог для подібних задач не існує єдиного алгоритму вирішення.

Однак це не означає, що подібні задачі не можуть бути вирішені в принципі, просто для їх вирішення необхідно використовувати різні підходи, нерідко творчі і нетрадиційні.

Приклад алгоритмічно нерозв’язної задачі: виявлення «мертвого коду».

1.9. Проблема відсутності загального методу вирішення задачі

Ця проблема визначає певний клас алгоритмічно нерозв’язних задач, приклади:

1. Розподіл дев’яток у запису числа π:

Визначимо функцію f(n) = i, де n – кількість цифр “9” підряд у десятковому запису числа π, а i – номер найбільш лівої дев’ятки із n тих, що йдуть підряд, наприклад: π =3,141592…; f(1) = 5

Задача полягає у визначенні f(n) для довільного n.

Оскільки число π є ірраціональним і трансцендентним, то ми не знаємо жодної інформації про розподіл дев'яток (так само як і будь-яких інших цифр) в десятковому записі числа. Обчислення f (n) пов'язане з обчисленням наступних цифр у розкладі π, до тих пір, поки ми не виявимо n дев'яток поспіль, однак у нас немає загального методу обчислення f (n), тому для деяких n обчислення можуть тривати нескінченно - ми навіть не знаємо в принципі (за природою числа π) чи існує рішення для всіх n.

2. Обчислення досконалих чисел

Досконалі числа – це числа, які дорівнюють сумі своїх дільників, наприклад: 28 = 1+2+4+7+14.

Визначимо функцію S (n) = n-е за рахунком досконале число і поставимо задачу обчислення S (n) по довільно заданому n.

Немає загального методу обрахунку досконалих чисел, невідомо навіть, чи множина досконалих чисел обраховна, чи ні, тому алгоритм має перебирати усі числа підряд, перевіряючи їх досконалість. Відсутність загального методу вирішення не дозволяє відповісти на питання про проблему зупинки: якщо ми перевірили M чисел під час пошуку n-го досконалого числа, чи може це означати, що його взагалі не існує?

3. Десята проблема Гільберта

Нехай задано многочлен n-го ступеня з цілими коефіцієнтами – P, чи існує алгоритм, який визначає, чи існує розв’язок рівняння P = 0 в цілих числах?

Математиками доведено, що такого алгоритму не існує, тобто загальний метод визначення цілих коренів рівняння P=0 по цілочисельним коефіцієнтам многочлену відсутній.

1.10. Проблема інформаційної невизначеності задачі

Позиціювання машини Поста на останню помічену скриньку.

Нехай на стрічці машини Поста задані набори помічених скриньок (кортежі) довільної довжини з довільними відстанями між кортежами, а головка знаходиться у самого лівого ящика. Задача полягає у встановленні головки на саму праву скриньку останнього кортежу.

Спроба побудови алгоритму вирішення задачі призводить до необхідності відповіді на питання – коли після визначення вправо на певну кількість M позицій і не знайшли початку наступного кортежу, чи означає це, що ще правіше бути вже помічених скриньок не може (стрічка нескінченна)?

Інформаційна невизначеність задачі у даному разі полягає у відсутності інформації чи про кількість кортежів на стрічці, чи про максимальну відстань між ними. За наявності такої інформації задача стає алгоритмічно вирішуваною.

1.11. Проблема логічної нерозв’язності задачі

Проблема еквівалентності алгоритмів. Дано два алгоритми (наприклад, дві машини Т’юринга). Необхідно визначити, чи будуть вони повертати однаковий результат на однакових вхідних даних?

Проблема тотальності. По довільному заданому алгоритму необхідно визначити, чи буде він зупинятися на всіх можливих наборах вхідних даних.

1.12. Побудова машини Т’юринга для обчислення деяких простих функцій

Розглянемо приклад простої машини Т’юринга.

Допустимо, ми маємо унарну систему числення:

Для якої описана наступна машина Т’юринга:

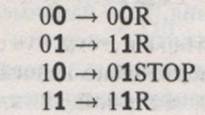
Пояснення: перша цифра (не виділена) зліва від стрілки означає стан, у якому машина знаходиться, а справа – стан, у який вона має перейти.

Виділена цифра зліва від стрілки – символ на стрічці, який в даний момент часу зчитує пристрій. Вона заміняє цей символ виділеною цифрою справа від стрілки.

R – означає, що пристрій має переміститися вздовж стрічки вправо, а L – вліво, STOP – зупинитися.

Навіщо потрібна дана машина?

Запустимо машину на наступній стрічці (початковий стан «0» і починає виконуватися з крайньої лівої позиції стрічки):

(Представлене на стрічці число представляє собою десяткове число «чотири»).

Розглянемо покрокове виконання машини:

– Машина зчитує «0», оскільки вона знаходиться у стані «0», то виконується наступна інструкція: 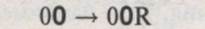, тобто машина записує на стрічку «0», переходить у стан «0» і переходить по стрічці вправо.

– …

– Машина зчитує «1», оскільки вона знаходиться у стані «0», то виконується наступна інструкція: 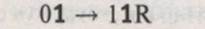, тобто машина записує на стрічку «1», переходить у стан «1» і переходить по стрічці вправо.

– Машина зчитує «1», оскільки вона знаходиться у стані «1», то виконується наступна інструкція: 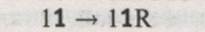, тобто машина записує на стрічку «1» переходить у стан «1» і переходить по стрічці вправо.

– …

– Машина зчитує «0», оскільки вона знаходиться у стані «1», то виконується наступна інструкція: 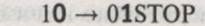, тобто машина записує на стрічку «1», переходить у стан «0» і зупиняється.

Який буде результат на стрічці?

1.13. Введення до оцінки складності алгоритмів

Одну і ту ж задачу можна вирішити багатьма способами, відповідно, може бути багато алгоритмів, які приводять до однакового результату за умов однакових вихідних даних.

Що може бути мірою якості алгоритму? Як один алгоритм можна вважати кращим за інший?

Складність – одна із характеристик алгоритму.

Який із алгоритмів кращий: простіший, чи складніший?

Нехай А — алгоритм розв'язання деякого класу задач, а N — розмірність окремої задачі цього класу. N може бути, наприклад, розмірністю оброблюваного масиву, числом вершин оброблюваного графа тощо,

Позначимо функцію fA(N), що дає верхню межу максимального числа основних операцій (додавання, множення і т. д.), які повинен виконати алгоритм А, розв'язуючи задачу розмірності N.

Тоді алгоритм А є поліноміальним, якщо fA(N) зростає не швидше, ніж деякий поліном від N. В іншому разі А — експоненціальний алгоритм.

Приклад: функції типу kn, kn², kn³,…, де k – коефіцієнт – поліноміальні; а функції виду kⁿ, nⁿ, n!.. - експоненціальні

У випадку традиційної Машини Т’юринга, яка ще має назву детермінованої (ДМТ), запис на стрічку, перехід каретки і зміна стану відбуваються однозначно визначено в залежності від стану машини і зчитаного нею символу.

У випадку недетермінованої Машини Т’юринга (НМТ) комбінація поточного стану машини та зчитаного символу на стрічці можуть допускати декілька переходів. Наприклад, якщо НМТ знаходиться у деякому стані 1 і зчитує символ “X”, то вона може як записати на стрічку символ Z і перейти в стан 2, так і записати на стрічку символ Y і перейти в стан 3.

Яким чином можна уявити НМТ? Існує два варіанти:

– Можна допустити, що НМТ є “виключно вдалою” і вона завжди обирає той перехід, який приводить до вирішення задачі.

– Можна уявити, що у випадку недетермінованого переходу (коли комбінація символу на стрічці і стану НМТ допускають декілька переходів) створюється копія машини (чи декілька копій, в залежності від кількості переходів), які далі функціонують паралельно.

Якщо ДМТ має єдиний шлях обчислень, то НМТ має “дерево обчислень”.

Алгоритми, складність яких є експоненціальною для ДМТ можуть мати поліноміальну складність для НМТ.

За своїми обчислювальними можливостями (здатністю вирішувати задачі) ДМТ і НМТ є еквівалентними.

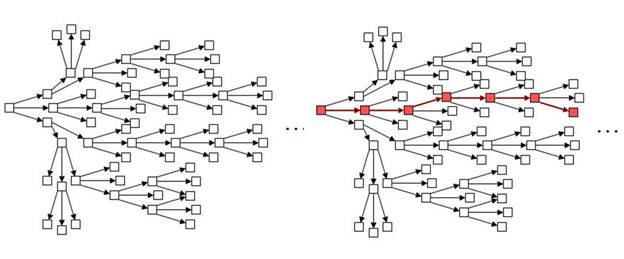
Рисунок 1.1 – Представлення НМТ у вигляді дерева варіантів

1.14. Визначення порядку складності алгоритму

До класу складності P належать задачі, які вирішуються за поліноміальний час за допомогою ДМТ

Що означає, що для стрічки ДМТ, у якій заповнено N комірок, необхідно здійснити не більше ніж T(N) переходів, де T(N) – деякий поліном від N

Згідно з О-нотацією, наступні задачі відносяться до класу складності P:

– Фіксований час: O(1)

– Лінійний час: O(N)

– Час за ступенем Y: O(N^Y)

– Логарифмічний час: О(log N)

Клас складності алгоритмів NP визначається аналогічно до P, але для НМТ:

До класу складності NP належать задачі, які вирішуються за поліноміальний час за допомогою НМТ

Згідно з О-нотацією, наступні задачі відносяться до класу складності NP:

– Експоненціальний час: O(Y^N)

– Час обчислення факторіалу: O(N!)

Задача перевірки, чи є число N розрядністю b складеним, НМТ вирішує за допомогою наступного алгоритму:

– 1. Обрати недетерміновано ціле число m, 1<m<N

– 2. Поділити націло N на m, залишок позначити через a

– 3. Якщо a=0, то повернути результат “ТАК”, інакше повернути “НІ”

Для наведеного алгоритму визначною частиною є час виконання ділення, який є поліноміальним – необхідно O(b²) кроків

Якщо для вирішення цієї задачі використовується ДМТ, то алгоритм слід модифікувати наступним чином:

– Від m:= 2, доки m<N:

o Поділити націло N на m, залишок позначити через a

o Якщо a=0, то повернути результат “ТАК” і закінчити виконання, інакше m:= m + 1

Як можна побачити, алгоритм для ДМТ буде експоненціальним, оскільки необхідно O(b²2^b) кроків

1.15. О-нотація для оцінки складності алгоритмів.

1.16. Фіксований час О(1).

1.17. Лінійний час О(N).

Дата добавления: 2014-01-04