Поняття оператора

Оператор – це закінчений вираз, який полягає у здійсненні обчислення, виклику методу, присвоювання значення, перевірки умови і т.д.

Оператори розділяються знаком “;”.

Приклад операторів:

j++;

y = x + b;

SomeClass.SomeFunc(par1, par2);

Складений оператор або блок являє собою декілька операторів, що поєднані фігурними дужками:

{

x1 = y1 + y2;

x2 = z1 + z2;

}

3.4. Прості оператори: присвоювання; виклику функції

Оператор присвоювання передбачає наявність змінної (зліва) і виразу (зправа), значення якого присвоюється змінній.

Приклад:

a = b + 12;

Оператор виклику функції (методу) передбачає наявність назви функції (методу) і, якщо необхідно, параметрів:

SomeFunc(SomePar);

Якщо параметри відсутні, то після назви функції слід залишати пусті дужки:

SomeFunc();

3.5. Оператори управління ходом виконання: розгалуження; вибору; цикли; переходу

Оператори управління ходом виконання дозволяють виконувати або не виконувати ділянки програми в залежності від певних умов.

Оператор розгалуження передбачає перевірку умови, в залежності від виконання якої (true) буде виконуватися один блок, а невиконання (false) – другий. Наявність другого блоку не є обов’язковою. Якщо у блоці має виконуватись один оператор, то оформлення його у вигляді складеного оператору (з фігурними дужками) не обов’язково.

Приклад:

if (a < 10)

{

j++;

b = a + c;

}

else

j--;

Оператор вибору (switch) – це оператор управління ходом виконання, який на основі умови передає керування одному із варіантів.

int caseSwitch = 1;

switch (caseSwitch)

{

case 1:

Console.WriteLine("Case 1");

break;

case 2:

Console.WriteLine("Case 2");

break;

default:

Console.WriteLine("Default case");

break;

}

Більш складний приклад використання switch:

class SwitchTest

{

static void Main()

{

Console.WriteLine("Coffee sizes: 1=Small 2=Medium 3=Large");

Console.Write("Please enter your selection: ");

string s = Console.ReadLine();

int n = int.Parse(s);

int cost = 0;

switch(n)

{

case 1:

cost += 25;

break;

case 2:

cost += 25;

goto case 1;

case 3:

cost += 50;

goto case 1;

default:

Console.WriteLine("Invalid selection. Please select 1, 2, or 3.");

break;

}

if (cost!= 0)

{

Console.WriteLine("Please insert {0} cents.", cost);

}

Console.WriteLine("Thank you for your business.");

}

}

Оператори циклів дозволяють повторно виконувати оператор (у тому числі складений оператор – блок) поки виконується певна умова, C# підтримує наступні варіанти циклів:

цикл do..while – передбачає повторне виконання оператору, доки вираз не прийме значення false

int x = 0;

do

{

Console.WriteLine(x);

x++;

} while (x < 5);

цикл while – передбачає виконання оператору, доки вираз не прийме значення false:

int n = 1;

while (n++ < 6)

{

Console.WriteLine("Current value of n is {0}", n);

}

цикл for (параметризований цикл) – передбачає виконання оператору, доки вираз не прийме значення false, при чому у операторі циклу задається змінна, значення якої буде змінюватися при кожній ітерації:

for (int i = 1; i <= 5; i++)

{

Console.WriteLine(i);

}

цикл foreach – передбачає виконання оператору над усіма елементами масиву чи колекції:

int[] fibarray = new int[] { 0, 1, 2, 3, 5, 8, 13 };

foreach (int i in fibarray)

{

System.Console.WriteLine(i);

}

Оператори переходу здійснюють безумовний перехід на певну ділянку коду.

Операторами переходу є:

break – призначений для завершення найближчого внутрішнього циклу чи оператору switch і переходу до наступного оператору, який йде за ним;

continue – передає керування на наступну ітерацію циклу, в якому він знаходиться;

return – перериває виконання методу, в якому він знаходиться і повертає керування методу, який його викликав. Якщо метод має повертати значення, то при виклику оператора слід вказати значення, що повертається, виклик оператору є обов’язковим. Якщо метод не передбачає повернення значення, то виклик цього оператору не є обов’язковим;

goto – здійснює перехід на певний іменований оператор (мітку). У сучасних програмах на C# найчастіше використовується лише в операторі switch для того, щоб перейти на інший варіант. У багатьох інших випадках використання цього оператору є вкрай небажаним, оскільки ставить під загрозу структуру програми.

3.6. Структурування програм: функції та класи

Для поділу коду програм на фрагменти з метою забезпечення повторного виклику, а також спрощення розробки, розуміння і збільшення наглядності, використовується підпрограми – іменовані блоки коду, які можуть бути викликані всередині операторів.

Підпрограми, які не повертають результат у точці виклику називаються процедурами і не можуть бути складовими виразів, а ті, які повертають, називаються функціями і можуть бути складовими виразів.

У сучасних об’єктно-орієнтованих мовах програмування будівельним блоком програм є більш комплексна і цілісна абстракція – клас, який являє собою поєднання коду і даних.

Підпрограми, які задекларовані всередині класу, називаються методами.

У мові програмування C# усі підпрограми декларуються в рамках класу, тому всі вони є методами.

3.7. Параметри функцій: вхідні, результуючі.

Повернення значень

Приклад:

Приклади повернення значення

Повернення об’єкту

Використання return для void-методів

Return може використовуватись для виходу із таких методів:

Формальні параметри:

Параметри за значенням

Виділення пам’яті для параметрів за значенням

Параметри за посиланням

Приклад використання параметрів за посиланням

Управління пам’яттю при використанні параметрів за посиланням

Параметри, які повертають значення

Приклад використання параметрів, які повертають значення

Управління пам’яттю при використанні параметрів, які повертають значення

Масиви параметрів

Варіанти виклику:

3.8. Рекурсивні функції

Рекурсія – дуже поширений у програмуванні підхід, який передбачає можливість виклику алгоритмом самого себе проте з іншими параметрами.

Вкладеність таких викликів може бути досить великою, проте в певний момент часу вона має припинитися і результат повертається (чи продовжуються обчислення) по ланцюгу рекурсивних викликів.

Основні переваги рекурсії:

рекурсія наглядна і зручна для представлення вирішення певних задач;

деякі структури природного чи штучного походження є рекурсивними за своєю сутністю;

деякі задачі є рекурсивними за своєю природою, зокрема рекурсія є окремим випадком декомпозиції – поділу однієї складної задачі на декілька простіших.

Приклади рекурсії

1. Натуральні числа:

1 – натуральне число;

ціле число, яке йде за натуральним, є натуральним числом.

2. Пісенька:

У попа був собака, він її любив

Вона з'їла шматок м'яса, він її убив

У землю закопав,

Напис написав:

«У попа був собака, він її любив

Вона з'їла шматок м'яса, він її убив

У землю закопав,

Напис написав:

«У попа був собака, він її любив

Вона з'їла шматок м'яса, він її убив

У землю закопав,

Напис написав:

…

Рекурсивне задання математичних функцій

Рекурсивно визначена функція містить у своєму визначенні посилання на саму цю функцію.

Розглянемо приклад визначення факторіалу.

Факторіал N:

N! = 1 × 2 × 3 × … × (N – 1) × N.

Рекурсивне визначення факторіалу:

N! = N × (N-1)!

Додатково:

0! = 1.

Числа Фібоначчі: елементи числової послідовності, в якій кожен наступний елемент дорівнює сумі двох попередніх:

FN = FN-1­ + FN-2, де N ≥ 2, F­0 = F1 = 1.

Приклад: 1, 1, 2, 3, 5, 8…

3. Поширені рекурсивні алгоритми

Бінарний пошук

Процедури обходу дерева

Фрактали – нескінченна самоподібна геометрична фігура, кожен фрагмент якої повторюється при зменшенні масштабу.

Задача про Ханойські вежі:

В одному з буддійських храмів ченці вже тисячу років займаються перекладанням кілець. Вони розташовані трьома пірамідами, на яких нанизані кільця різних розмірів. У початковому стані 64 кільця були нанизані на першу піраміду й упорядковані по розмірі. Ченці повинні перекласти всі кільця з першої піраміди на другу, виконуючи єдину умову - кільце не можна покласти на кільце меншого розміру. При перекладанні можна використовувати всі три піраміди. Ченці перекладають одне кільце за одну секунду. Як тільки вони закінчать свою роботу, наступить кінець світу.

Рекурсивний алгоритм обчислення факторіалу

using System;

using System.Collections.Generic;

using System.Text;

namespace Factorial

{

class Program

{

public static long fact(long n)

{

if (n == 0)

{

return 1;

}

else

{

return n * fact(n - 1);

}

}

static void Main(string[] args)

{

for (int i = 0; i <= 20; i++)

{

Console.WriteLine("{0}! = {1}", i, fact(i));

}

Console.ReadLine();

}

}

}

Алгоритм Евкліда для знаходження найбільшого спільного дільника

Число n є дільником числа m, якщо число m ділиться на число n без остачі.

Дільники числа 18: 1, 2, 3, 6, 9, 18.

Дільники числа 24: 1, 2, 3, 4, 6, 12, 24.

Найбільший спільний дільник чисел 18 та 24 це 6.

Скорочено: НСД (18, 24) = 6.

НСД (m, n) це найбільше з чисел на яке діляться і m і n.

Два числа m та n називаються взаємно простими, якщо їх НСД (m, n)=1. Наприклад, НСД(9, 16)=1.

Алгоритм Евкліда дозволяє знайти НСД двох натуральних чисел.

Суть алгоритму Евкліда – два числа порівнюють, та з більшого віднімають менше до тих пір, поки числа не стануть рівними. Число, якому вони стануть рівними і є їх найбільший спільний дільник.

using System;

using System.Collections.Generic;

using System.Text;

namespace Example

{

class Program

{

public static int nsd(int m, int n)

{

if (m == n)

{

return m;

}

else

{

if (m > n)

{

return nsd(m - n, n);

}

else

{

return nsd(n - m, m);

}

}

}

static void Main(string[] args)

{

Console.WriteLine(nsd(873435, 21345).ToString());

Console.ReadLine();

}

}

}

6. Рекурсивний алгоритм для обчислення чисел Фібоначчі

using System;

using System.Collections.Generic;

using System.Text;

namespace Example

{

class Program

{

public static long Fibonacci(long N)

{

if ((N == 1) | (N == 0))

{

return 1;

}

else

{

return Fibonacci(N - 1) + Fibonacci(N - 2);

}

}

static void Main(string[] args)

{

for (int i = 0; i <= 30; i++)

{

Console.WriteLine("{0}, {1}", i, Fibonacci(i));

}

Console.ReadLine();

}

}

}

3.9. Файли: текстові, бінарні

Питання 2. Операції над бінарними файлами

Відкриття файлу

Перш ніж почати роботу з файлами необхідно використати простір імен System.IO:

using System.IO;

1. Процедура відкриття файлу здійснюється наступним чином:

FileStream fs = new FileStream("test.data", FileMode.CreateNew);

Перший параметр – ім’я файлу, другий параметр – режим, у якому відкривається файл.

Перелік доступних режимів (FileMode):

Append;

Create;

CreateNew;

Open;

OpenOrCreate;

Truncate.

2. Створення пристрою для доступу:

BinaryWriter w = new BinaryWriter(fs);

3. Виконання операцій по запису інформації до файлу:

for (int i = 0; i < 11; i++)

{

w.Write((int)i);

}

4. Закриття файлу:

w.Close();

fs.Close();

Програма, яка записує значення до файлу і зчитує їх

using System;

using System.IO;

namespace Simple

{

class App

{

public static void Main()

{

string fname = "test.data";

if (File.Exists(fname))

{

File.Delete(fname);

}

// Запис даних

FileStream fs = new FileStream(fname, FileMode.CreateNew);

BinaryWriter w = new BinaryWriter(fs);

for (int i = 0; i < 11; i++)

{

w.Write((int)i); // Вказуємо тип даних

}

w.Close();

fs.Close();

// Зчитування даних

fs = new FileStream(fname, FileMode.Open, FileAccess.Read);

BinaryReader r = new BinaryReader(fs);

for (int i = 0; i < 11; i++)

{

Console.WriteLine(r.ReadInt32()); // Вказуємо тип даних

}

r.Close();

fs.Close();

Console.ReadKey(); // Чекаємо натискання клавіші

}

}

}

Вміст файлу

Доступ до довільних елементів файлу

Якщо необхідно зчитувати не всі елементи файлу, а перейти до елементу з певним номером, можна використати метод Seek потоку:

fs.Seek(sizeof(Int32)*8, SeekOrigin.Begin);

Текстові файли відрізняються від бінарних тим, що передбачають збереження текстової інформацією у рядках, які закінчуються службовими символами закінчення рядку.

Зчитування і запис текстового файлу здійснюється по рядкам.

Приклад запису інформації до текстового файлу

using System;

using System.IO;

public class TextToFile

{

private const string FILE_NAME = "MyFile.txt";

public static void Main(String[] args)

{

if (File.Exists(FILE_NAME))

{

Console.WriteLine("{0} already exists.", FILE_NAME);

return;

}

using (StreamWriter sw = File.CreateText(FILE_NAME))

{

sw.WriteLine("This is my file.");

sw.WriteLine("I can write ints {0} or floats {1}, and so on.",

1, 4.2);

sw.Close();

}

}

}

Приклад читання інформації із текстового файлу

using System;

using System.IO;

public class TextFromFile

{

private const string FILE_NAME = "MyFile.txt";

public static void Main(String[] args)

{

if (!File.Exists(FILE_NAME))

{

Console.WriteLine("{0} does not exist.", FILE_NAME);

return;

}

using (StreamReader sr = File.OpenText(FILE_NAME))

{

String input;

while ((input=sr.ReadLine())!=null)

{

Console.WriteLine(input);

}

Console.WriteLine ("The end of the stream has been reached.");

sr.Close();

}

}

Лекція 4. Алгоритми чисельних методів, апроксимації функцій, інтегрування та вирішення рівнянь з одним невідомим

Перелік питань

1. Чисельні методи.

2. Особливості вирішення задач чисельними методами, точність та коректність рішень.

3. Апроксимації функцій: лінійна інтерполяція; інтерполяційний многочлен Ньютона.

4. Чисельне інтегрування: метод трапецій; метод Сімпсона; метод Сімпсона з оцінкою погрішності.

5. Вирішення рівнянь з одним невідомим: метод простих ітерацій; метод Ньютона; метод парабол.

4.1. Чисельні методи

Чисельні методи — методи наближеного або точного розв'язування задач, які ґрунтуються на побудові послідовності дій над скінченною множиною чисел.

У програмуванні та алгоритмізації чисельні методи – це математичний інструментарій, за допомогою якого математична задача формулюється у вигляді, зручному для розв’язання на комп’ютері. У такому разі говорять про перетворення математичної задачі в обчислювальну задачу. При цьому послідовність виконання необхідних арифметичних і логічних операцій визначається алгоритмом її розв’язання. Алгоритм повинен бути ітеративним (рекурсивним) і складатися з відносно невеликих блоків, які багаторазово виконуються для різних вхідних даних.

Основні риси чисельних методів:

– передбачають проведення великої кількості рутинних арифметичних обчислень за допомогою рекурсивних співвідношень, які використовуються для організації ітерацій (повторюваних циклів обчислень із зміненими початковими умовами для поліпшення результату);

– направлені на локальне спрощення задачі (наприклад, лінеаризація нелінійних обчислень);

– залежать від близкості початкового наближення

4.2. Особливості вирішення задач чисельними методами, точність та коректність рішень

Використання чисельних методів має певні особливості.

Зокрема, у процесі вирішення задачі виникає похибка, викликана наступними причинами:

Неточний математичний опис задачі, зокрема, вихідні дані.

Неточний метод, який використовується для задачі (використання чисельних методів само собою передбачає обмежену кількість розрахунків, а не нескінченну, яка необхідна для отримання точного результату, однак неможлива на сучасних ЕОМ).

При введенні даних і виконанні обчислень за допомогою ЕОМ відбуваються округлення.

Відповідно похибка буває:

p1 - Така, що не можна усунути:

• викликана неточністю числових даних, які входять у математичний опис задачі;

• є наслідком невідповідності математичного опису задачі реальності – похибка математичної моделі.

p2 - Похибка метода

p3 - Похибка обчислення

Повна похибка: p0 = p1 + p2 + p3.

Повна похибка визначає різницю між фактично отриманим і точним рішенням задачі.

4.3. Апроксимації функцій: лінійна інтерполяція; інтерполяційний многочлен Ньютона.

Апроксимація функцій – типова прикладна сфера використання чисельних методів, полягає у заміні оригінальної функції наближеною.

Потреба в апроксимації виникає найчастіше у ситуаціях, коли розрахунок оригінальної функції є трудомістким, а апроксимований (наближений) варіант є прийнятним.

Лінійна інтерполяція (метод хорд) – використовується у ситуаціях, коли функція лінійно залежить від параметрів. Полягає у інтерполяції P1(x) = ax + b функції f, що задана в двух точках x0 и x1 відрізку [a, b].

Виходячи з формули прямої:

Отримаємо для

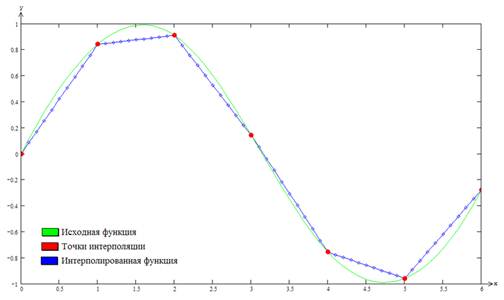
Рисунок 4.1 – Приклад кусково-лінійної інтерполяції

Приклад коду для виконання лінійної інтерполяції

static double interpolate(double x0, double y0, double x1, double y1, double x)

{

return y0 * (x - x1) / (x0 - x1) + y1 * (x - x0) / (x1 - x0);

}

Пояснення: у вигляді параметрів задаються значення двох відомих аргументів і результатів функції (відповідно x0, x1 та y0, y1), а також значення аргументу (x), для якого необхідно здійснити інтерполяцію

Інтерполяційний многочлен Ньютона

У ситуації, коли лінійна інтерполяція не дає очікуваних результатів, слід застосувати інші (нелінійні) методи, одним за найпоширеніших серед яких є інтерполяційний многочлен Ньютона.

Якщо дано k+1 точок даних: (де значення xj не повторюються)

То комбінація поліномів Ньютона буде являтися інтерполяцією функції:

де:

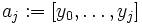
якщо

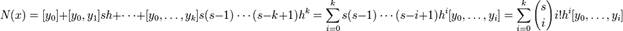
4.4. Чисельне інтегрування: метод трапецій; метод Сімпсона; метод Сімпсона з оцінкою погрішності.

Інтеграл: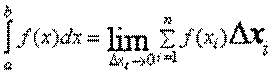

Можна замінити:

1. Метод прямокутників: замінюємо графік функції F(x) горизонтальною лінією, обчислюємо інтеграл як площу прямокутників , де h – крок інтегрування, y0 – значення функції при x0

Рисунок 4.2 – Чисельне інтегрування методом прямокутників

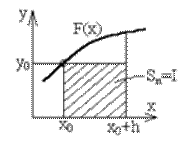
Рисунок 4.3 – Розрахунок площі прямокутника і трапеції

2. Метод трапецій: здійснюємо аналогічну заміну, але прямою, яка проходить через дві точки (x0, y0) та (x0 + h, y1), обчислюємо інтеграл як площу трапеції

Метод Сімпсона

Замінюємо графік функції F(x) квадратичною параболою, яка проходить через три точки з координатами (х0,у0), (х0+h,у1), (х0+2h,у2). Розрахункову формулу для обчислення елементу інтегральної суми визначають, виходячи із лінійної інтерполяції:

Рисунок 4.4 – Графічне представлення методу Сімпсона

Загальні функції по методам:

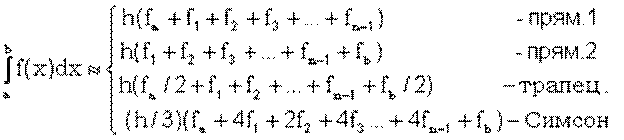
4.5. Вирішення рівнянь з одним невідомим: метод простих ітерацій; метод Ньютона; метод парабол.

Існує формула для вирішення квадратного рівняння, рівняння третього ступеня.

Як щодо рівняння четвертого ступеня? П’ятого?

Для вирішення багатьох рівнянь, аналітичне рішення яких є складним, громіздким, або взагалі неможливим, на допомогу приходять чисельні методи.

Метод простих ітерацій.

При вирішенні рівняння методом простих ітерацій використовується запис його у вигляді x = f(x). Задаються початкове значення аргументу x0 та наближення ε. Перше наближення x1 знаходиться із виразу x1 = f(x0), друге – x2 = f(x1) і т.д. У загальному випадку i+1 наближення знаходиться по формулі xi + 1 = f(xi). Зазначена процедура повторюється, доки |f(xi) > ε |. Умова сходимості метода ітерацій: |f'(x)|<1.

Опис алгоритму: доки | f(xi) > ε виконувати xi+1 =f(xi).

Лекція 5. Алгоритми вирішення системи лінійних рівнянь, пошуку екстремуму функції

Перелік питань

1. Вирішення системи лінійних рівнянь методом Гауса.

2. Пошук екстремуму функцій одної змінної: метод золотого перетину; метод парабол.

3. Пошуку екстремуму функцій багатьох змінних: метод координатного спуску; метод найскорішого спуску.

5.1. Вирішення системи лінійних рівнянь методом Гауса

Представимо систему лінійних рівнянь наступним чином:

Далі, здійснюючи елементарні перетворення, приведемо матрицю до трикутного вигляду:

Далі, починаючи з найнижчого рівняння слід визначати корінь, підставляти його у вище рівняння і т.д. до останнього.

Процес елементарних перетворень здійснюється наступним чином: із другого рівняння віднімається перше, помножене на таке число, щоб зник коефіцієнт при x1. Потім таким же чином віднімемо перше рівняння із третього, четвертого і т.д. Тоді будуть виключені всі коефіцієнти першого стовбця, які знаходяться нижче головної діагоналі. Далі, використовуючи друге рівняння, виключаються коефіцієнти другого стовбця і т.д.

Опис алгоритму

На першому етапі (прямий хід) матрицю приводять до трикутної форми, чи визначають, що система не є сумісною. Робиться це наступним чином: серед елементів першого стовпця обирають ненульовий, переміщують його у крайнє верхнє положення перестановкою рядків і віднімають отриманий після перестановок перший рядок із інших, помножив його на величину, яка дорівнює відношенню першого елемента кожного із цих рядків до першого елемента першого рядку, обнуляючи стовбець під ним. Після того, як вказані перетворення здійснені, перший рядок і перший стовпець подумки викреслюють і продовжують до тих пір, доки не залишиться матриця нульового розміру. Якщо на якійсь з ітерацій серед елементів першого стовпця не знайшовся нульовий, то переходять до наступного.

На другому етапі (зворотній хід) слід виразити рішення системи рівнянь. Процедура починається з останнього рівняння, із якого виражають базисну змінну і підставляють у вище рівняння, піднімаючись таким чином нагору.

Приклад роботи алгоритму

Необхідно вирішити наступну систему лінійних рівнянь:

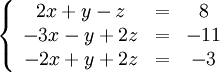
Обнулимо коефіцієнти біля x у другому та третьому рядках. Для цього помножимо перший рядок на 2/3 та 1 відповідно і складемо з першим рядком:

Аналогічно поступимо із коефіцієнтом при y у третьому рядку (множимо другий рядок на -6 і складаємо з третім):

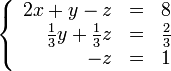
Таким чином система приведена до трикутного вигляду.

На зворотньому ході вирішемо рівняння, починаючи з нижнього:

z = -1

y = 3

x = 2

Приклад коду

using System;

public class Gaussian

{

public static void Main()

{

int n = 0;

string data;

Console.WriteLine("\n****** Gaussian Eminination ******");

//input # of equations

Console.Write("Input number of euqations:");

data = Console.ReadLine();

n = int.Parse(data);

double[,] a = new double[n, n];

double[] b = new double[n];

double x, sum;

//input matrix coefficients

for (int i = 0; i < n; i++)

for (int j = 0; j < n; j++)

{

Console.Write("Input matrix coefficients a[" + i + "," + j + "]=");

data = Console.ReadLine();

a[i, j] = double.Parse(data);

}

//input right-hand side vector

for (int i = 0; i < n; i++)

{

Console.Write("Input right-hand side vecotr b[" + i + "]=");

data = Console.ReadLine();

b[i] = double.Parse(data);

}

Console.WriteLine("Coefficient matrix:");

printMatrix(a, n);

Console.WriteLine("\nRigh-hand side vector:");

printVector(b, n);

//convert to upper triangular form

for (int k = 0; k < n - 1; k++)

{

try

{

for (int i = k + 1; i < n; i++)

{

x = a[i, k] / a[k, k];

for (int j = k + 1; j < n; j++)

a[i, j] = a[i, j] - a[k, j] * x;

b[i] = b[i] - b[k] * x;

}

}

catch (DivideByZeroException e)

Console.WriteLine(e.Message);

}

/* back substitution */

b[n - 1] = b[n - 1] / a[n - 1, n - 1];

for (int i = n - 2; i >= 0; i--)

{

sum = b[i];

for (int j = i + 1; j < n; j++)

sum = sum - a[i, j] * b[j];

b[i] = sum / a[i, i];

}

Console.WriteLine("Solution:");

printVector(b, n);

} // Main()

public static void printMatrix(double[,] a, int n)

{

for (int i = 0; i < n; i++)

{

for (int j = 0; j < n; j++)

Console.Write(a[i, j].ToString("F4") + "\t");

Console.WriteLine();

}

Console.WriteLine();

}

public static void printVector(double[] b, int n)

{

for (int i = 0; i < n; i++)

Console.Write(b[i].ToString("F4") + "\t");

Console.WriteLine("\n");

}

}

5.2. Пошук екстремуму функцій одної змінної: метод золотого перетину; метод парабол.

Припустимо, що нам задано інтервал, на якому слід здійснити пошук мінімуму функції. Розмістимо на цьому інтервалі дві точки симетрично до його центру і здійснено обчислення функції у них:

Рисунок 5.1 – Золотий перетин

Якщо f(x1) < f(x2), то права частина вилучається і мінімум слід шукати на лівій частині інтервалу:

Рисунок 5.2 – Пошук на лівій частині інтервалу

Оскільки одна точка і обчислене значення вже є, то на відрізку слід встановити наступну точку (також симетрично) і повторити ітерацію:

Рисунок 5.3 – Повторення ітерації

Визначення координат кожної наступної точки здійснюється, виходячи із наступного співвідношення: τ / 1 = (1 – τ) / τ, звідки випливає, що 1 – τ = τ2 Далі можна визначити τ = (-1 ± √5)/2, позитивне значення: τ = 0,61803…

Таким чином використовуючи значення τ, або (1 – τ), помножене на довжину інтервалу, можна визначити координати наступної точки.

Назву цей метод отримав із-за принципом поділу інтервалу який має назву “золотий перетин” і часто використовується у мистецтві, архітектурі і т.д.

Метод парабол

Метод парабол дозволяє апроксимувати функцію поліномом і отримати краще наближення до значення екстремуму.

Опис алгоритму:

Обираємо на досліджуваному інтервалі три точки u1, u2, u3, такі, що u1 < u2 < u3

Будуємо параболу: Q(u) = a0 + a1 (u - u1) + a2 (u - u1)(u - u2), графік якої проходить через точки (u1,f(u1)), (u2,f(u2)), (u3,f(u3)). Коефіцієнти ak, k = 1, 2, 3 знаходяться із системи рівнянь: Q(u1) = f(u1), Q(u2) = f(u2), Q(u3) = f(u3), звідки:

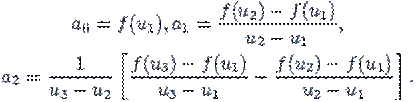
Точку u мінімуму Q(u) знаходять, прирівнявши його похідну до нуля:

Отримана точка приймається за наступне наближення, інші дві точки обираються із відповідних точок інтервалу [u1, u3]

5.3. Пошук екстремуму функцій багатьох змінних: метод координатного спуску; метод найскорішого спуску.

Пошук екстремуму (мінімуму) функції багатьох змінних F(x1, x2,.., xk)за методом координатного спуску полягає у почерговому пошуку мінімуму по координаті x1, далі по координаті x2 і т.д. Пошук здійснюється з однаковим кроком, який зменшується після знаходження наближених значень по всім координатам для уточнення рішення.

У загальному випадку, для того, щоб знайти точку x* локального мінімуму функції F(x(k)), складають послідовність точок (наближених рішень) {x(k)}, яка сходиться до точки x*.

Крок обирається таким чином, щоб:

xn+1(k)=xn(k) + h (1)

при

F (xn+1(k))<F (xn(k)) (2)

та

xn+1(k)=xn(k) – h (3)

при

F (xn+1(k))>F (xn(k)) (4)

Обчислення припиняють, коли досягається задана точність: |xn+1(k) – xn(k)| < e

Для пошуку екстремуму по одній координаті використовуються ті ж методи, що й для пошуку екстремуму однієї змінної (наприклад, метод золотого перетину).

Метод найскорішого спуску (градієнтів)

Метод найскорішого спуску для пошуку мінімуму функції багатьох змінних реалізує ітераційну процедуру руху до мінімуму функції із довільно обраної точки початкового наближення у напрямку найбільш сильного зменшення функції.

Цей напрямок є протилежним вектору градієнта, який формується із похідних функції по всім її аргументам.

Приклад: вектор градієнта функції f (x, y, z) = 2x + 3y2 – sin z буде (2, 6y, -cos z)

Алгоритм:

Обчислюються складові вектору градієнту в черговій i-й точці (Xi)

Складається функція f[Xi - a grad f(Xi)] однієї змінної a.

Здійснюється пошук мінімуму f[Xi - a grad f(Xi)] → min a

Визначаються координати чергової точки:

Якщо умова зупинки (|xn+1(k) – xn(k)| < e) не виконується, то переходять на крок 1.

Рисунок 5.4 – Графічне представлення методу градієнтів

Приклад програмного коду: http://is.gd/b9TAi

Лекція 6. Алгоритми обробки масивів

Перелік питань:

1. Визначення масивів.

2. Операції з масивами.

3. Упорядкування масивів: сортування вибором; сортування вставкою; бульбашкове сортування; сортування методом Шелла; метод швидкого сортування.

4. Вибір методів сортування.

5. Пошук в упорядкованих масивах методом половинного поділу, інтерполяційним методом.

6. Застосування індексів для пошуку у невпорядкованих даних.

6.1. Визначення масивів

Масив – базова регулярна впорядкована структура даних для зберігання значення одного типу

Доступ до елементів масиву є прямим, здійснюється за один крок за допомогою індексу

Масив може бути одновимірним чи багатовимірним.

Масив займає повний обсяг відведеного на нього пам’яті, незалежно від того, скільки елементів записано до нього

Операції запису і зчитування елементу з конкретним індексом з масиву є швидкими

Операція зміни розміру масиви, вставки/видалення елемента із зсувом усіх інших є повільними

Декларація і доступ до елементів масиву у C#

Декларація масиву у C# відбувається наступним чином:

int[] Integers;

Декларація і створення одномірного масиву розміром 100 значень:

int[] Integers = new int[100];

Для доступу до елемента масиву слід вказати його ідентифікатор і індекс:

Integers[50] = 12345;

Індексація елементів масиву починається з 0, тому перший елемент має індекс 0, а останній – розмірність масиву мінус 1.

Ініціалізація масиву під час декларації

Під час декларації масиву можна ініціалізувати його, наприклад:

string[] DaysOfTheWeek = { "Sunday", "Monday", "Tuesday", "Wednesday", "Thursday", "Friday", "Saturday" };

Декларація багатовимірних масивів

Декларація багатовимірних прямокутних масивів здійснюється наступним чином (наприклад, декларація та ініціалізація двовимірного масиву рядків):

string[,] StudentNameGrade = { {"Петренко", "Відмінно"},

{"Луценко", "Задовільно"},

{"Шевченко", "Добре"}

};

Декларація ортогональних масивів здійснюється наступним чином:

int[][][] Integers;

6.2. Операції над масивами

Для отримання довжини одновимірного масиву використовується конструкція:

int ArrayLength = Integers.Length;

Для багатовимірного масиву використовується метод GetLength(), у параметрах якого слід вказати номер виміру (починаючи з 0):

int multiArrLength = StudentNameGrade.GetLength(0);

Для сортування масиву використовується наступна конструкція (викликається статичний метод Sort() стандартного класу Array, якому передається масив, що необхідно відсортувати, у якості параметру):

Array.Sort(Integers);

Для зміни порядку елементів масиву на зворотній використовується наступна конструкція:

Array.Reverse(Integers);

Обробка всього масиву

Якщо необхідно звернутися до всіх елементів масиву, то зробити це можна в циклі, або використати ітератор.

Виведення всіх елементів масиву на екран, використовуючи цикл:

for (int i = 0; i < Integers.Length; i++)

{

Console.WriteLine(Integers[i].ToString());

}

Виведення всіх елементів масиву на екран, використовуючи ітератор:

foreach (int item in Integers)

{

Console.WriteLine(item.ToString());

}

6.3. Упорядкування масивів: сортування вибором; сортування вставкою; бульбашкове сортування; сортування методом Шелла; метод швидкого сортування.

Сортування – процес перестановки об’єктів у певному порядку.

Основне призначення сортування – полегшення пошуку об’єктів.

Існує велика кількість алгоритмів сортування, одного «найкращого» до нинішнього часу не винайдено. Вибір підходящого алгоритму залежить від характеру даних, їх розподілу, пам’яті, у якій вони зберігаються.

Наприклад, поширеним є поділ алгоритмів сортування на:

– внутрішні – сортування масивів і даних в оперативній пам’яті;

– зовнішні – сортування даних у файлах.

На рис. 6.1 умовно представлено сортування масиву, на рис. 6.2 – сортування файлу.

Рисунок 6.1 – Сортування масиву

Рисунок 6.2 – Сортування файлу

За зміною порядку елементів розрізняють:

– стійке сортування – при виконанні алгоритму на відсортованому наборі даних порядок елементів не змінюється;

– нестійке сортування – при виконанні алгоритму на відсортованому наборі даних порядок елементів змінюється.

Ключ – елемент даних, за яким здійснюється сортування. Для ключа має використовуватися такий тип даних, для якого існує спосіб визначення порядку елементів.

Складність виконання алгоритму – кількість операцій, а також обсяг додаткової пам’яті, необхідної для його виконання.

Найпростіший алгоритм сортування водночас є неефективним (нерозумним), його складність О(n³):

using System;

using System.Collections.Generic;

using System.Text;

namespace SortApplication

{

class Program

{

static void swap(int[] arr, int i, int j)

{

int t = arr[i];

arr[i] = arr[j];

arr[j] = t;

}

static void stupidSort(int[] arr)

{

int i = 0;

while (i < arr.Length - 1)

{

if (arr[i + 1] < arr[i])

{

swap(arr, i, i + 1);

i = 0;

}

else

{

i++;

}

}

}

static void Main(string[] args)

{

int[] testArr = { 44, 55, 12, 42, 94, 18, 06, 67};

stupidSort(testArr);

foreach (int i in testArr)

{

Console.Write("{0} ", i);

}

Console.ReadLine();

}

}

}

Інший варіант нерозумного сортування – сортування Акульшина: генеруються всі можливі перестановки масиву, для яких здійснється перевірка правильного порядку. Складність: О (n × n!).

Алгоритм сортування вставками

Основна ідея алгоритму полягає в тому, щоб поступово впорядковувати масив, вставляючи нові елементи у вже впорядковану частину (рис. 6.3). Складність алгоритму – О (n²).

Рисунок 6.3 – Схематичне представлення роботи алгоритму сортування простими вставками

Код програми:

using System;

using System.Collections.Generic;

using System.Text;

namespace SortingApplication

{

class Program

{

static void insertSort(int[] a)

{

int i, j, value;

for (i = 1; i < a.Length; i++)

{

value = a[i];

for (j = i - 1; (j >= 0) && (a[j] > value); j--)

{

a[j + 1] = a[j];

}

a[j + 1] = value;

}

}

static void Main(string[] args)

{

int[] testArr = {44, 55, 12, 42, 94, 18, 06, 67};

insertSort(testArr);

foreach (int i in testArr)

{

Console.Write("{0} ", i);

}

Console.ReadLine();

}

}

}

Результат виконання програми (рис. 6.4).

Рисунок 6.4 – Результат виконання програми

Особливості алгоритму – простий і наглядний в реалізації, однак ресурсоємний.

Модифікований варіант даного алгоритму – сортування бінарними вставками оснований на тому, що у вже відсортованій частині масиву елементи можна включати, виконуючи бінарний пошук.

Алгоритм бульбашкового сортування

Алгоритм бульбашкового сортування передбачає повторні проходи по масиву, який сортується. За кожен прохід елементи порівнюються попарно і якщо порядок серед двох елементів невірний, то здійснюється обмін елементів. Проходи по масиву виконуються до тих пір, доки не стане зрозуміло, що обміни елементів вже не потрібні, тобто масив відсортований.

Свою назву алгоритм отримав за принципом роботи – у процесі його виконання елемент, який стоїть не на власному місці, «спливає» до необхідної позиції наче бульбашка у воді.

Схематично робота алгоритму представлена на рис. 11.3.

Складність алгоритму – О(n²).

Рисунок 6.5 – Схематичне представлення роботи алгоритму бульбашкового сортування

Код програми, яка виконує бульбашкове сортування:

using System;

using System.Collections.Generic;

using System.Text;

namespace SortApplication

{

class Program

{

static void swap(int[] arr, int i, int j)

{

int t = arr[i];

arr[i] = arr[j];

arr[j] = t;

}

static void bubbleSort(int[] arr)

{

for (int i = arr.Length - 1; i > 0; i--)

{

for (int j = 0; j < i; j++)

{

if (arr[j] > arr[j + 1])

{

swap(arr, j, j + 1);

}

}

}

}

static void Main(string[] args)

{

int[] testArr = {44, 55, 12, 42, 94, 18, 06, 67};

bubbleSort(testArr);

foreach (int i in testArr)

{

Console.Write("{0} ", i);

}

Console.ReadLine();

}

}

}

Модифікації алгоритму:

– виявлення проведених обмінів;

– шейкер-сортування.

Алгоритм сортування за методом Шелла

Ідея алгоритму – необхідно порівнювати елементи, які знаходяться не тільки поряд, а і на відстані один від одного. Спочатку порівнюються і сортуються між собою ключі, які стоять на певній відстані d. Після цього процедура повторюється для деяких менших значень d, і так до тих пір, доки d не стане рівним одному, у такому разі робота методу буде ідентична сортуванню простими вставками.

Схематично робота алгоритму представлена на рис. 6.6.

Складність алгоритму: O(n log n)

Рисунок 6.6 – Схематичне представлення роботи алгоритму

Код програми:

using System;

using System.Collections.Generic;

using System.Text;

namespace SortApplication

{

class Program

{

static void shellSort(int[] arr)

{

int j;

int step = arr.Length / 2;

while (step > 0)

{

for (int i = 0; i < (arr.Length - step); i++)

{

j = i;

while ((j >= 0) && (arr[j] > arr[j + step]))

{

int tmp = arr[j];

arr[j] = arr[j + step];

arr[j + step] = tmp;

j--;

}

}

step = step / 2;

}

}

static void Main(string[] args)

{

int[] testArr = {44, 55, 12, 42, 94, 18, 06, 67};

shellSort(testArr);

foreach (int i in testArr)

{

Console.Write("{0} ", i);

}

Console.ReadLine();

}

}

}

Особливості алгоритму – за звичайних обставин кількість порівнянь є меншою, ніж у алгоритмів сортування вставками та бульбашкового сортування.

Алгоритм швидкого сортування

Алгоритм швидкого сортування або алгоритм сортування Хоара – найшвидший серед відомих алгоритмів сортування загального призначення. Розроблений англійським інформатиком Чарльзом Хоаром. Швидшими за нього є лише спеціалізовані алгоритми, які побудовані з урахуванням специфіки даних, для яких вони використовуються.

Ідея алгоритму основана на принципі «поділяй і володарюй»:

1. Обираємо деякий елемент, який буде називатися опорним елементом.

2. Здійснюємо операцію поділу масиву: реорганізуємо його таким чином, щоб всі елементи менші чи рівні опорному були зліва від нього, а всі більші – справа.

3. Рекурсивно за цим же алгоритмом впорядковуємо списки елементів, які знаходяться зліва і справа від опорного.

Складність алгоритму: в середньому – О(n log n), найгірший випадок – О (n²).

Код програми:

using System;

using System.Collections.Generic;

using System.Text;

namespace SortApplication

{

class Quicksort

{

public static void qsort(int[] items)

{

qs(items, 0, items.Length - 1);

}

static void qs(int[] items, int left, int right)

{

int i, j;

int x, y;

i = left; j = right;

x = items[(left + right) / 2];

do

{

while ((items[i] < x) && (i < right))

{

i++;

}

while ((x < items[j]) && (j > left))

{

j--;

}

if (i <= j)

{

y = items[i];

items[i] = items[j];

items[j] = y;

i++; j--;

}

} while (i <= j);

if (left < j)

{

qs(items, left, j);

}

if (i < right)

{

qs(items, i, right);

}

}

}

class Program

{

static void Main(string[] args)

{

int[] testArr = {44, 55, 12, 42, 94, 18, 06, 67};

Quicksort.qsort(testArr);

foreach (int i in testArr)

{

Console.Write("{0} ", i);

}

Console.ReadLine();

}

}

6.4. Вибір методів сортування

Вибір підходящого алгоритму сортування залежить від декількох умов:

– Кількість операцій (складність алгоритму)

– Доступність пам’яті (у тому числі для реалізації рекурсії)

– Вимоги до стійкості алгоритму

– Швидкість доступу на запис/читання даних

– Характер даних

– і т.д.

У загальному випадку – якщо не підходить алгоритм швидкого сортування Хоара, відомий як найшвидший серед алгоритмів сортування загального призначення, то слід обрати інший алгоритм, враховуючи існуючі обмеження.

6.5. Пошук в упорядкованих масивах методом половинного поділу, інтерполяційним методом

Пошук – операція, яка дуже часто здійснюється при роботі з інформацією

У процесі пошуку (вибірки) необхідно знайти один чи декілька елементів, які задовольняють певним вимогам (значенню одного чи декількох ключів)

Під час реалізації пошуку необхідно сприймати до уваги наступне:

– для пошуку дуже важливою є швидкість його виконання, алгоритми пошуку мають масштабуватися відповідно до росту обсягів даних;

– в окремих випадках доступ до самих даних у процесі виконання пошуку може бути ускладнений(наприклад, недопустимо повільний), тому власне процедура пошуку має здійснюватися у спеціальних допоміжних даних (індексах);

– у багатьох випадках пошук здійснюється частіше, ніж додавання нових даних, тому у процесі додавання даних можна здійснювати операції, які полегшують пошук (підтримка індексу);

– іноді пошук має здійснюватися за неповним співпаданням з ключем;

– іноді результатів пошуку може бути настільки багато, що необхідно знаходити способи впорядкування результатів за значимістю.

Послідовний пошук за допомогою повного перебору елементів

Послідовний пошук за допомогою повного перебору елементів – найпростіша реалізація пошуку, однак вона є і найповільнішою.

В окремих ситуаціях подібна реалізація пошуку є неможливою чи недоцільною.

Підходить для відносно невеликих обсягів даних, які зберігаються в оперативній пам’яті

Приклад реалізації послідовного пошуку повним перебором елементів масиву

class Program

{

struct Student

{

public string Name;

public string Group;

}

static Student[] studArr;

static void InitArray()

{

studArr = new Student[3];

studArr[0] = new Student() {Name = "Іванов", Group = "ЕК-01"};

studArr[1] = new Student() { Name = "Петров", Group = "ЕК-02" };

studArr[2] = new Student() { Name = "Сидоров", Group = "ЕК-03" };

}

static int Find(string Name)

{

for (int i = 0; i < studArr.Length; i++)

{

if (studArr[i].Name == Name)

{

return i;

}

}

return -1;

}

Приклад реалізації послідовного пошуку повним перебором елементів (продовж.)

static void Main(string[] args)

{

InitArray();

Console.WriteLine("Введіть прізвише студента для пошуку");

string NameToFind = Console.ReadLine();

int StudIdx = Find(NameToFind);

if (StudIdx!= -1)

{

Console.WriteLine("Студента знайдено: індекс у масиві - {0}, група - {1}", StudIdx, studArr[StudIdx].Group);

}

else

{

Console.WriteLine("Студента не знайдено");

}

Console.ReadLine();

}

}

Пошук шляхом перебору сортованих послідовностей елементів

Послідовний пошук повним перебором елементів у сортованих списках спрощується за рахунок того, що елементи у них впорядковані, і якщо ми здійснюємо пошук у списку, відсортованому у порядку зростання елементів, і зустрічаємо елемент зі значенням ключа більшим, ніж шукаємо, то пошук можна припинити, оскільки елемент знайти вже не вдасться

Відповідно модифікуємо метод Find попереднього прикладу:

4. Двійковий пошук

Якщо пошук необхідно здійснювати у відсортованій послідовності елементів, то значно кращим, ніж послідовний перебір є використання двійкового пошуку

Двійковий пошук суттєво скорочує кількість операцій, які необхідно виконати у процесі пошуку, однак можливий лише для таких структур даних, у яких можливий довільний доступ (наприклад, масиви), однак неприйнятний до структур даних із послідовним доступом (наприклад, зв’язані списки)

Приклад реалізації бінарного пошуку

Приклад реалізації бінарного пошуку (продовж.)

Інтерполяційний пошук

Якщо елементи у впорядкованій послідовності розподілені відносно рівномірно (особливо характерно для великих обсягів даних), то пошук можна істотно пришвидшити завдяки тому, щоб прогнозувати позицію елемента даних

Прогноз можна зробити, виходячи із значення елемента, кількості елементів у діапазоні та значень першого і останнього елемента послідовності

Пошук, оснований на такому підході, має назву інтерполяційного, його можливості і обмеження використання дуже близькі до бінарного, однак на великих наборах даних він може працювати значно швидше

Особливо помітні переваги інтерполяційного пошуку при роботі з даними, розміщеними на повільних носіях даних

Приклад реалізації інтерполяційного пошуку

Слідкуючий пошук

В певних випадках необхідно здійснити пошук декількох елементів у послідовності. Для того, щоб пришвидчити пошук можна скористатися алгоритмами слідкуючого пошуку (hunt search), які дозволяють скористуватись даними попереднього пошуку для здійснення нового пошуку

В найпростішій реалізації слідкуючого пошуку необхідно порівняти елемент, який шукався останнім, із наступним і відповідним чином розпочати новий пошук до чи після нього

В залежності від алгоритму, який використовується, слідкуючий пошук може бути бінарним чи інтерполяційним

7. Реалізація оптимізованого пошуку у впорядкованих текстових даних

Найпростіший прийнятний у більшості випадків варіант для текстових даних – бінарний пошук

Використання інтерполяційного пошуку ускладнено у зв’язку з тим, що у ньому використовуються розрахунки, основані на значеннях елементів, що напряму з текстовими даними зробити неможливо.

Проте інтерполяційний пошук можна реалізувати також і з текстовими даними, однак для цього необхідно використати спеціальні алгоритми, за допомогою яких текстові рядки можна закодувати і отримати числа придатні для розрахунків. Алгоритм кодування має бути таким, щоб отримані числа не були занадто великими для розрахунків, однак відповідали порядку сортування текстових даних

6.6. Застосування індексів для пошуку у невпорядкованих даних

Індекси – додаткові допоміжні дані, які створюються для прискорення пошуку

Індекси доцільно використовувати у випадках:

Коли задача реалізації пошуку є пріоритетною

Коли порядок даних не можна змінювати

Коли дані розміщені у пам’яті з повільним доступом

Використання індексів передбачає певну попередню підготовчу роботу для побудови індексу, а також підтримки його у актуальному стані, коли поновлюються дані

Найпоширенішими є індекси на основі різних варіантів дерев, зокрема, бінарних та Б-дерев

Лекція 7. Алгоритми обробки даних на основі списків та дерев

План лекції

1. Визначення списку.

2. Види списків: незалежні списки, однозв’язані списки; двозв’язані списки; кільцеві списки; упорядковані списки.

3. Основні операції над списками: включення елементу до списку; видалення елементу; перехід між елементами; ітератор для списку.

4. Упорядкування та пошук в списках.

5. Похідні структури даних: черга, стек, дек.

6. Визначення дерева.

7. Впорядковані дерева.

8. Бінарні дерева.

9. Основні операції з бінарними деревами: включення елементу; видалення елементу; обхід дерева.

10. Балансування дерева.

11. Б-дерева.

Дата добавления: 2014-01-04