Визначення дерева

Дерево - одна з найпоширеніших структур даних. Формально дерево визначається як скінченна множина Т з однієї або більше вершин (вузлів, nodes), яке задовольняє наступним вимогам:

1. існує один виокремлений вузол - корень (root) дерева

2. інші вузли (за виключенням кореня) розподілені серед m ≥ 0 непересічних множин T₁...T_m і кожна з цих множин в свою чергу є деревом. Дерева T₁...T_m мають назву піддерев (subtrees) даного кореня.

Графічне зображення дерева представлено на рис. 7.5.

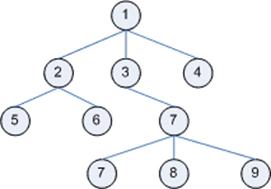
Рисунок 7.5 – Графічне зображення дерева

З цього визначення випливає, що кожна вершина є в свою чергу коренем деякого піддерева. Кількість піддерев вершини має назву ступеня (degree) цієї вершини. Вершина ступеню нуль має назву кінцевої (terminal) або листа (leaf). Некінцева вершина також має назву вершини розгалуження (branch node). Нехай x - довільна вершина дерева з коренем r. Тоді існує єдиний шлях з r до x. Усі вершини на цьому шляху називаються предками (ancestors) x; якщо деяка вершина y є предком x, то x називається нащадком (descendant) y. Нащадки та предки вершини x, що не співпадають з нею самою, називаються власними нащадками та предками. Кожну вершину x, в свою чергу, можна розглядати як корень деякого піддерево, елементами якого є вершини-нащадки x. Якщо вершини x є предком y та не існує вершин поміж ними (тобто x та y з'єднані одним ребром), а також існують предки для x (тобто x не є коренем), то вершина x називається батьком (parent) до y, а y - дитиною (child) x. Коренева вершина єдина не має батьків. Вершини, що мають спільного батька, називаються братами (siblings). Вершини, що мають дітей, називаються внутрішніми (internal). Глибиною вершини x називається довжина шляху від кореня до цієї вершини. Максимальна глибина вершин дерева називається висотою.

Лісом (forest) називають множину дерев, які не перетинаються.

Найчастіше дерева в інформатиці зображують з коренем, який знаходиться зверху (говорять, що дерево в інформатиці "росте вниз").

Важливими операціями на деревах є:

– обхід вершин в різному порядку;

– перенумерація вершин;

– пошук елемента;

– додавання елемента у визначене місце в дереві;

– видалення елемента;

– видалення цілого фрагмента дерева;

– додавання цілого фрагмента дерева;

– трансформації (повороти) фрагментів дерева;

– знаходження кореня для будь-якої вершини.

Найбільшого розповсюдження ці структури даних набули в тих задачах, де необхідне маніпулювання з ієрархічними даними, ефективний пошук в даних, їхнє структуроване зберігання та модифікація.

Існують різні сфери використання та способи представлення дерев.

Графічне представлення дерева у вигляді множини представлено на рисунку 7.6.

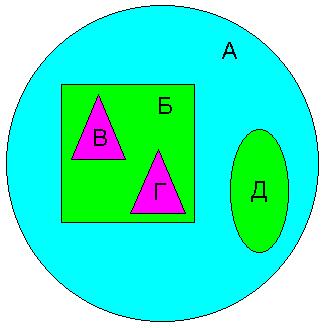
Рисунок 7.6 – Графічне представлення дерева у вигляді множини

Більш формально представлення дерева у вигляді множини можна сприймати наступним чином: вершина Б є дочірньою по відношенню до вершини А в тому разі, якщо діапазон чисел вершини Б лежить всередині діапазону вершини А.

Представлення дерева у вигляді вкладених дужок:

(V0(V1(V2(V5)(V6))(V3)(V4))(V7(V8)(V9(V10))))

Представлення дерева у вигляді графа (рисунок 7.7).

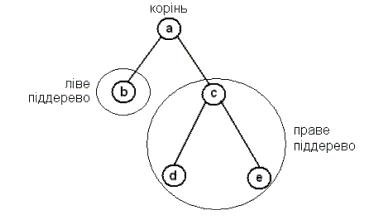
Рисунок 7.7 – Представлення дерева у вигляді графа

Представлення дерева у вигляді списку з уступами (рисунок 7.8).

Рисунок 7.8 – Представлення дерева у вигляді списку з уступами

Представлення дерева у вигляді десяткової системи Д’юі (рисунок 7.9)

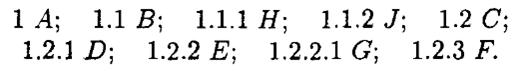
Рисунок 7.9 – Представлення дерева у вигляді десяткової системи Д’юі

Представлення дерева у вигляді діаграми Венна (рисунок 7.10)

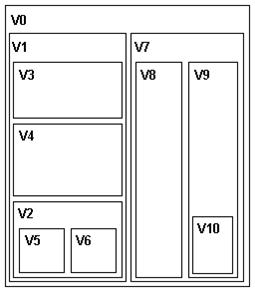
Рисунок 7.10 – Представлення дерева у вигляді діаграми Венна

Обхід дерева

Обхід дерева – одна з найпоширеніших операцій з деревами.

Передбачає відвідування усіх вершин дерева, при цьому кожна вершина відвідується один раз.

Існують різні способи здійснення обходу дерева: обхід у глибину з використанням рекурсії, обхід у глибину без використання рекурсії, обхід у ширину та ін.

7.7. Впорядковані дерева

Дерево вважається орієнтованим, якщо воно задовольняє наступним вимогам:

– у дерева існує один корінь;

– кожен вузол дерева може бути досягнутий із кореня.

Дерево вважається впорядкованим, якщо порядок його елементів є фіксованим.

Наприклад, структура папок і файлів є орієнтованим впорядкованим деревом.

7.8. Бінарні дерева

Бінарне дерево - це динамічна структура даних, що складається з вузлів (елементів), кожен з яких містить, окрім даних, не більше двох посилань на інші бінарні дерева. На кожен вузол припадає рівно одне посилання. Початковий вузол називається коренем дерева (рисунок 6.7).
Якщо дерево організоване таким чином, що для кожного вузла всі ключі його лівого піддерева менші за ключ цього вузла, а всі ключі його правого піддерева - більші, воно називається деревом пошуку. Однакові ключі в деревах пошуку не допускаються.

В дереві пошуку можна знайти елемент за ключем, рухаючись від кореня і переходячи на ліве або праве піддерево в залежності від значення ключа в кожному вузлі. Такий спосіб набагато ефективніший пошуку по списку, так як час виконання операції пошуку визначається висотою дерева.
Дерево є рекурсивною структурою даних, так як кожне піддерево є також деревом. Дії з такими структурами даних простіше всього описувати за допомогою рекурсивних алгоритмів.

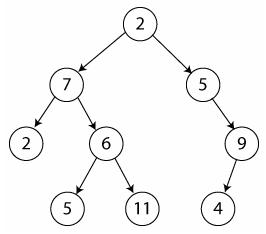
Рисунок 7.11 – Бінарне дерево

7.9. Основні операції з бінарними деревами: включення елементу; видалення елементу; обхід дерева

Існують три види таких обходів, кожний яких визначається рекурсивно:

Прямий порядок (preorder) наступної послідовності:

1. відвідати корінь

2. відвідати ліве піддерево

3. відвідати праве піддерево

Тобто, в такому порядку обходу кожна вершина відвідується до того, як будуть відвідані її діти.

Зворотний порядок (postorder) наступної послідовності:

1. відвідати ліве піддерево

2. відвідати праве піддерево

3. відвідати корінь

Тобто, в такому порядку кожна вершина відвідується лише після того, як будуть відвідані її діти.

Центрований (центральний) порядок (inorder) наступної послідовності:

1. відвідати ліве піддерево

2. відвідати корінь

3. відвідати праве піддерево

В такому порядку кожна вершина відвідується між відвіданням лівої та правої дитини. Такий порядок особливо часто застосовується в бінарних деревах пошуку, тому що дає можливість обходу вершин у порядку збільшення їхніх порядкових номерів.

На рисунку зображено, яким чином здійснюється обхід бінарного дерева:

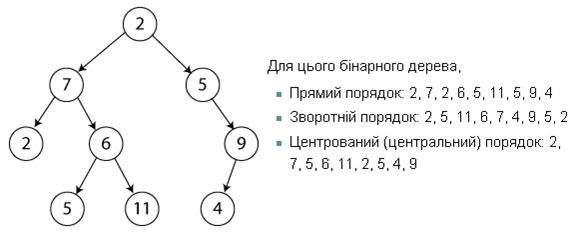
Рисунок 7.12 – Різні варіанти обходу бінарного дерева

Прямий обхід (префіксний обхід, обхід в глибину «зверху вниз»):

– Почати з кореня дерева.

– Помітити поточну вершину

– Здійснити прямий обхід лівого піддерева

– Здійснити прямий обхід правого піддерева.

Прямий обхід подано на рисунку.

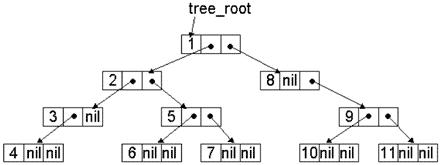
Рисунок 7.13 – Прямий обхід дерева

Зворотній обхід (постфіксний обхід, обхід в глибину «знизу вгору»):

1. Почати з кореня дерева.

2. Здійснити зворотній обхід лівого піддерева.

3. Здійснити зворотній обхід правого піддерева.

4. Помітити поточну вершину.

Зворотній обхід подано на рисунку.

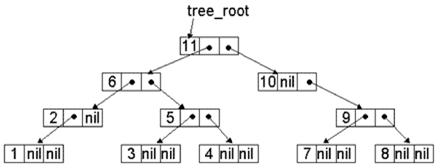
Рисунок 7.14 – Зворотній обхід

Центрований обхід (синтаксичний обхід, інфіксний обхід, обхід «зліва направо»):

1. Почати з кореня дерева

2. Здійснити прямий обхід лівого піддерева

3. Помітити поточну вершину

4. Здійснити прямий обхід правого піддерева

Центрований обхід подано на рисунку.

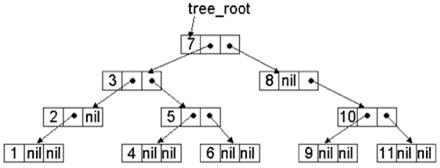
Рисунок 7.15 – Центрований обхід

Обхід в ширину:

– Помітити корінь дерева

– Помітити всі вершини 1-го рівня (зліва направо)

– Помітити всі вершини 2-го рівня

– …

Варіант алгоритму обходу в ширину:

– Занести (і помітити) в чергу корінь дерева

– Доки черга не стане пустою повторювати наступні дії:

2.1. Видалити перший елементи із голови черги.

2.2. Додати (і помітити) в хвіст черги всіх потомків видаленої черги

Включення елементу до дерева

Розглянемо приклад реалізації бінарного дерева

using System;

using System.Collections.Generic;

using System.Text;

namespace Tree

{

class Node

{

public String Data = null;

public Node Parent = null;

public Node LeftChild = null;

public Node RightChild = null;

public void SetLeftChild(Node aLeftChild)

{

this.LeftChild = aLeftChild;

if (aLeftChild!= null)

{

aLeftChild.Parent = this;

}

}

public void SetRightChild(Node aRightChild)

{

this.RightChild = aRightChild;

if (aRightChild!= null)

{

aRightChild.Parent = this;

}

}

//Конструктор для вершин з дітьми

public Node(Node aLeftChild, Node aRightChild)

{

this.SetLeftChild(aLeftChild);

this.SetRightChild(aRightChild);

}

// Конструктор для вершин без дітей

public Node()

{

Parent = null;

this.SetLeftChild(null);

this.SetRightChild(null);

}

}

class Program

{

static void Main(string[] args)

{

Node a = new Node();

Node b = new Node();

Node c = new Node(a, b);

}

}

}

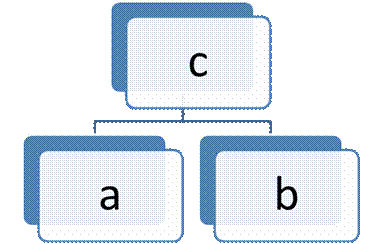
Рисунок 7.16 – Приклад дерева

Включення елементу d між елементами c та b:

class Program

{

static void Main(string[] args)

{

Node a = new Node();

Node b = new Node();

Node c = new Node(a, b);

Node d = new Node();

d.SetLeftChild(b);

c.SetRightChild(d);

}

}

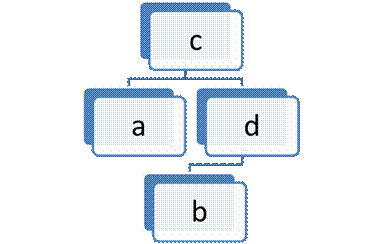
Рисунок 7.17 – Приклад включення елемента

Прямий обхід дерева:

// Прямий обхід

public static void PreorderTravel(Node current)

{

if (current!= null)

{

Console.WriteLine(current.Data);

PreorderTravel(current.LeftChild);

PreorderTravel(current.RightChild);

}

}

Створення дерева і виконання обходу:

Node a = new Node();

a.Data = "5";

Node b = new Node();

b.Data = "11";

Node c = new Node(a, b);

c.Data = "6";

Node d = new Node();

d.Data = "2";

a = new Node(d, c);

a.Data = "7";

c = new Node();

c.Data = "4";

d = new Node(c, null);

d.Data = "9";

c = new Node(null, d);

c.Data = "5";

b = new Node(a, c);

b.Data = "2";

PreorderTravel(b);

Результат:

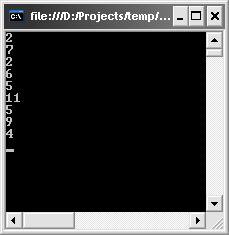
Рисунок 7.16 – Результат виконання прямого обходу

Центрований обхід:

// Центрований обхід

public static void CenterOrderTravel(Node current)

{

if (current!= null)

{

CenterOrderTravel(current.LeftChild);

Console.WriteLine(current.Data);

CenterOrderTravel(current.RightChild);

}

}

На тому ж дереві:

CenterOrderTravel(b);

Результат:

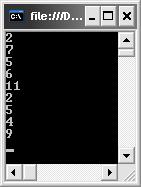
Рисунок 7.17 – Результат виконання центрованого обходу

Зворотній обхід:

// Зворотній обхід

public static void ReverseOrderTravel(Node current)

{

if (current!= null)

{

ReverseOrderTravel(current.LeftChild);

ReverseOrderTravel(current.RightChild);

Console.WriteLine(current.Data);

}

}

На тому ж дереві:

ReverseOrderTravel(b);

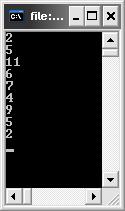
Рисунок 7.17 – Результат виконання зворотнього обходу

Пошук по дереву з включенням

Основна сфера використання бінарних дерев – реалізація алгоритмів бінарного пошуку (такі дерева мають назву бінарних дерев пошуку, BST).

Побудова бінарного дерева пошуку здійснюється шляхом виконання процедури, яка має назву «пошук по дереву з включенням» - у її реалізації здійснюється пошук елемента в дереві, і якщо його не знайдено, то елемент розміщується у необхідній позиції на дереві.

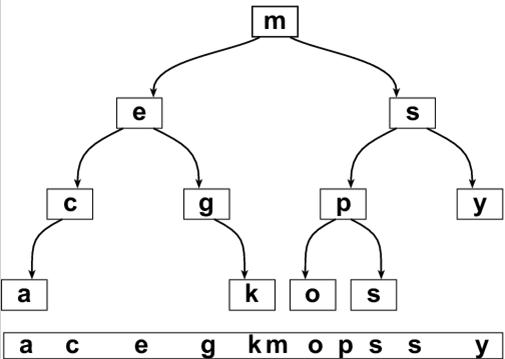
Рисунок 7.18 – Бінарне дерево пошуку

Видалення із дерева:

class Program

{

static void Main(string[] args)

{

Node a = new Node();

Node b = new Node();

Node c = new Node(a, b);

// Включення вузла d

Node d = new Node();

d.SetLeftChild(b);

c.SetRightChild(d);

// Повернення до попереднього варіанту дерева

c.SetRightChild(b);

}

}

Дата добавления: 2014-01-04