Балансування дерева

В програмуванні збалансоване дерево в загальному розумінні цього слова - це такий різновид бінарного дерева пошуку, яке автоматично підтримує свою висоту, тобто кількість рівнів вершин під коренем, мінімальною. Ця властивість є важливою тому, що час виконання більшість алгоритмів на бінарних деревах пошуку пропорційний до їхньої висоти, і звичайні бінарні дерева пошуку можуть мати досить велику висоту в тривіальних ситуаціях. Процедура зменшення (балансування) висоти дерева виконується за допомогою трансформацій, відомих як обернення дерева, в певні моменти часу (переважно при видаленні або додаванні нових елементів).

Ідеально збалансованим деревом є таке, у якого для кожної вершини різниця між висотами лівого та правого піддерев не перевищує одиниці. Однак, така умова доволі складна для виконання на практиці і може вимагати значної перебудови дерева при додаванні або видаленні елементів.

Тому було запропоноване менш строге визначення, яке отримало назву умови АВЛ(AVL)-збалансованості і говорить, що бінарне дерево є збалансованим, якщо висоти лівого та правого піддерев різняться не більше ніж на одиницію. Дерева, що задовольняють таким умовам, називаються AVL-деревами. Зрозуміло, що кожне ідеально збалансоване дерево є також АВЛ-збалансованим, але не навпаки.

Ідеально збалансовані дерева є ресурсоємними для балансування, тому звичайно балансування здійснюється для АВЛ-дерев.

Кожна вершина АВЛ-дерева зберігає різницю між висотами для лівого і правого піддерев. У збалансованому дереві ця величина може приймати лише одне з трьох значень: -1, 0, 1. Якщо значення відрізняється від вказаного, то дерево необхідно балансувати.

Дерево (піддерево), яке потребує балансування, балансується за допомогою операції обертання вліво чи вправо:

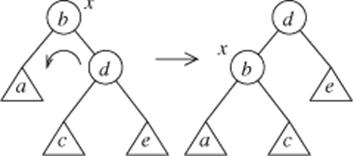
Рисунок 7.19 – Обертання дерева вліво

Рисунок 7.20 – Обертання дерева вправо

Приклад балансування дерева шляхом обертання:

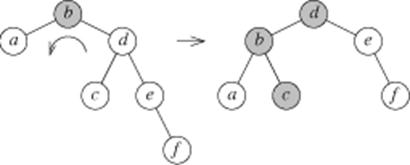
Рисунок 7.21 – Балансування дерева шляхом обертання

Алгоритм:

1. Проводиться розмітка дисбалансу вузлів.

2. Знаходиться нижній вузол з . (позначається Ш_i)

3. Для Ш_i розглядається сусідні вузли 2-го порядка.

4. Здійснюються оператори обертання

5. Проводиться операція зв’язування, яка не порушує АВЛ-відносин.

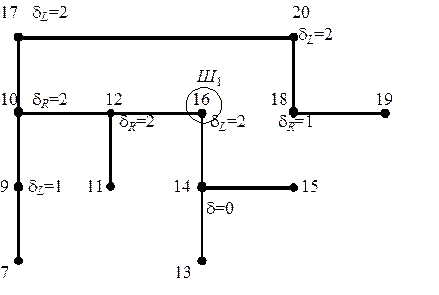
1) Підняти Ш ₁ 2) Опустити Ш ₂

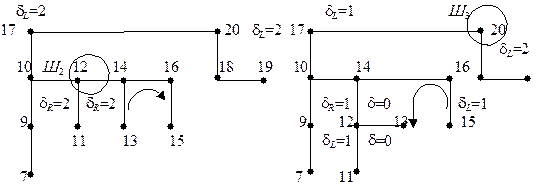
1) Підняти Ш ₃

Рисунок 7.22 – Балансування дерева

Дата добавления: 2014-01-04