Мощности предприятий

Автор: Вилисов Валерий Яковлевич, профессор кафедры Математики Технологического университета (г. Королев, Моск. обл.)

Задача размещения с ограничениями по

Задача размещения без ограничений

Модели размещения производства

Модели этого типа имеют несколько приложений в экономической практике, например:

• размещения предприятий;
• размещения складов;
• размещения филиалов банка;
• размещение пунктов обработки (приемки) и переработки отходов;
• размещение поставщиками текущих партий товара в тех или иных из арендуемых складов.

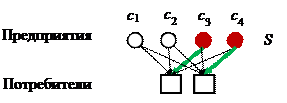
Постановка задачи размещения предприятий, производящих некоторую однородную продукцию, имеет такой вид.

Задано множество пунктов возможного размещения предприятий (или других объектов размещения) 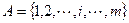. При этом известны затраты на размещение предприятия в каждом из этих пунктов - .

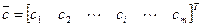Известно множество потребителей - и соответствующие им объемы потребностей в продукции на интервале времени 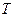. Заданы и затраты на производство и доставку продукции потребителю 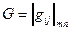в пределах интервала времени .

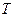Задача размещения заключается в выборе множества пунктов размещения таким образом, чтобы суммарные издержки были минимальными. При этом подмножество 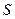предприятий из множества 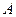может быть любым в количестве от 1 до 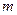. Ограничения на мощность предприятий не накладываются.

Целевая функция имеет вид:

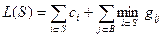
Отсюда критерий:

.

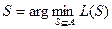Параметры и данные задачи можно представить и в табличном виде:

A	ci	B
		…	j	…	n
	c 1	g 11	g 12	…	g 1 j	…	g 1 n
	c2	g 21	g22	…	g2 j	…	g 2 n
…	…	…	…	…	…	…	…
i	ci	gi 1	gi 2	…	gij	…	gin
…	…	…	…	…	…	…	…
m	cm	gm1	gm 2	…	gmj	…	gmn
	Σ ci	min gi 1	min gi 2	…	min gij	…	min g 1 j

Первое слагаемое в ЦФ – это единовременные издержки, а второе – издержки производства (и логистики), где суммируются издержки по всем потребителям, а каждое слагаемое соответствует издержкам того предприятия из множества 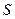, для которого они минимальны.

Эта задача относится к комбинаторной оптимизации, для которых, как правило, нет общих методов решения, а часто используются эвристические процедуры. Если размерность задачи небольшая, то ее можно решить простым перебором вариантов.

Пример. Пусть имеется 3 места размещения, т.е. 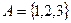и 2 потребителя, т.е. . Вектор единовременных затрат 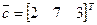. Матрица издержек производства и логистики:

.

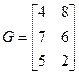Решим эту задачу перебором вариантов. Все варианты подмножеств 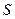следующие:

.

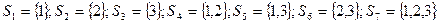Вычислим все значения ЦФ:

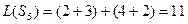
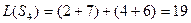
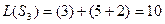
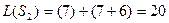
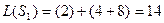
Наименьшим суммарным издержкам соответствует вариант .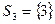

?

Для этого варианта задачи кроме данных предыдущей модели вводятся следующие элементы:

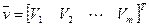- вектор максимально возможных объемов производства (предельной производительности) в пунктах размещения;

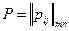- матрица потребностей j -го потребителя в продукции i -го предприятия.

Вводятся также следующие переменные:

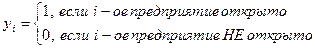
ЦФ для этой задачи имеет вид:

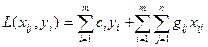
Тогда задача оптимального размещения примет вид:

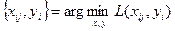
при ограничениях:

1. каждый потребитель может обслуживаться только одним производством:

;

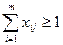2. суммарный объем потребностей всех потребителей любого j -го производства не должен превышать его предельной производительности:

;

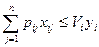3. искомые переменные могут принимать только булевы значения:

.

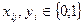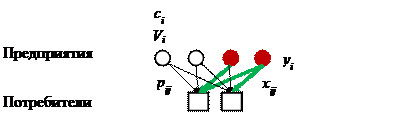
Эта задача относится к классу задач целочисленного (булева) линейного программирования и может быть решена одним из методов условной оптимизации.

Дата добавления: 2014-01-04