Модель одношагового распределения средств

Автор: Вилисов Валерий Яковлевич, профессор кафедры Математики Технологического университета (г. Королев, Моск. обл.)

Элементы диверсификации

Одним из путей выживания предприятий в рыночной среде является диверсификация – т.е. создание или развитие новых бизнесов, а это тесно связано с управлением инвестициями.

При диверсификации решают такие задачи как:

· выбор множества развиваемых бизнесов;

· выбор источников финансирования новых бизнесов;

· распределение ограниченных финансовых ресурсов между бизнесами и этапами.

При выборе бизнеса выполняются следующие оценки:

1. Привлекательность отрасли, которая заключается в ее способности давать устойчиво высокие доходы на инвестиции.

2. Стоимость входа в целевую отрасль не должна быть настолько высокой, чтобы нейтрализовать потенциал хорошей прибыльности.

3. Возможность улучшения, т.е. новый бизнес должен предоставить дополнительное конкурентное преимущество прежнему бизнесу компании.

Диверсификация может происходить двумя путями:

1. внедрение в технологически близкий (родственный) бизнес;

2. вступление в существенно отличающийся бизнес.

Диверсификация родственного плана возможна при технологической совместимости функционирующего и нового бизнеса. Важным финансовым фактором родственной диверсификации является значительная экономия затрат на производство продукции. Родственная диверсификация может осуществляться на основе следующих общих моментов:

· аналогичные сектора рынка по потребителям,

· соответствие производственных циклов,

· аналогичный характер менеджмента.

Стратегия неродственной диверсификации базируется на финансовых критериях, что позволяет исключить малоприбыльную деятельность за счет более эффективного использования активов.

Каждый бизнес, выбираемый для диверсификации, характеризуется набором показателей, например:

· прибыль;

· период окупаемости;

· время выхода на проектную мощность;

· степень риска провала;

· и др.

Показатели могут оцениваться экспертами и/или с помощью специальных моделей (например, в Project Expert).

Если невозможно оценить значения показателей на длительную перспективу, то можно решать задачу одношагового распределения (ЗОР) средств между бизнесами (направлениями, программами, проектами, …). При этом ЗОР может решаться многократно на очередной плановый период.

Возможны разные принципы распределения средств, крайние из которых такие:

1. Распределить средства на все бизнесы пропорционально их значимости.

2. Все средства направить на один наиболее важный бизнес.

Рассмотрим варианты реализации этих принципов.

П р и м е р.

Пусть имеются 4 программы инвестирования, для каждой из которых построены оценки трех показателей. Все показатели имеют одинаковую важность.

Показатели	Бизнесы
Планируемая прибыль
Оценка риска	0.3	0.2	0.4	0.8
Средняя зарплата

Для каждого бизнеса определить его весовой коэффициент относительной значимости, т.е. для всех найти вектор весов 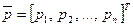. При этом в зависимости от принципа распределения средства могут быть разделены пропорционально весам или направлены на самый значимый.

?

Если необходимо выбрать только один бизнес для финансирования, то можно воспользоваться методами многокритериальной оптимизации – выбрать вариант (бизнес), оптимальный по множеству критериев (показателей).

Если надо распределить средства пропорционально весам, то можно воспользоваться методами экспертного оценивания. При этом оценки бизнесов по каждому из показателей следует рассматривать как оценки отдельного эксперта. Тогда задачу вычисления весов можно решать с помощью обработки данных групповой экспертизы. В первой части курса рассмотрены два таких метода:

1. Сложение ранжировок.

2. Вычисление медианы (или средней) Кемени.

Рассмотрим оба варианта в применении к инвестированию.

1. Вычисление весов путем сложения ранжировок.

Значения показателей (матрица 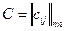) обычно бывают представлены в различных абсолютных шкалах и могут быть разнонаправленными (min или max).

Показатели	Бизнесы	Критерий
		…	n
Показатель 1	c 11	c 12	…	c 1 n	max
Показатель 2	c 21	c 22	…	c 2 n	min
…	…	…	…	…	…
Показатель m	cm 1	cm 2	…	cmn	max
Веса	p 1	p 2	…	pn	max

Общая схема вычисления вектора весов 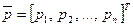заключается в том, чтобы каждую строку матрицы С преобразовать нормированный вектор, а затем их сложить и получить искомый вектор весов.

Реализуем алгоритм в виде следующих этапов.

Этап 1. Привести все критерии к одному виду, например, max, для чего строки матрицы C, соответствующие критериям на min, умножить на (-1). Далее будем считать, что все показатели на max.

Этап 2. По каждому показателю – т.е. для каждой строки матрицы C вычислить наименьший элемент:

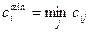
Этап 3. Каждый элемент в каждой строке матрицы C уменьшить на величину 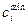(т.е. выполнить операцию сдвига):

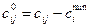
Этап 4. В каждой строке выполнить нормировку, в результате которой будет получена матрица весов 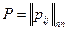, состоящая из строк-весов объектов (бизнесов) по показателям:

.

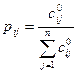Для всех элементов строк матрицы Р будут выполняться свойства:

; .

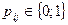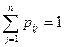Этап 5. Вычислить искомые веса бизнесов построчным сложением элементов матрицы Р:

,

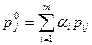где 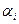- коэффициент значимости i -го показателя.

Здесь веса 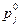не нормированы. Для нормировки необходимо пересчитать:

.

?

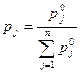П р и м е р. (продолжение)

После преобразований исходной матрицы получим результирующую матрицу весов Р при условии, что все :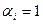

Показатели (i)	Бизнесы (j)
Планируемая прибыль		0.33	0.11	0.56
Оценка риска	0.33	0.40	0.27
Средняя зарплата		0.17	0.50	0.33
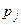	0.111	0.300	0.293	0.296

Таким образом, на основании полученного вектора весов инвестиционный ресурс может распределяться одним из двух способов:

1. Весь ресурс на самый значимый бизнес – (j =2).

2. Ресурс выделяется пропорционально весам .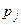

?

2. Вычисление весов на основе медианы Кемени.

Мера Кемени, как расстояния между ранжировками, позволяет более строго свернуть в одну все ранжировки-показатели.

Поскольку по каждой ранжировке можно построить матрицу парных сравнений (МПС) и наоборот, то вычисление вектора весов (для распределения инвестиций) возможно двумя способами:

1. С использованием меры Кемени для МПС.

2. С использованием меры Кемени непосредственно для ранжировок.

Для каждого из этих вариантов исходным «сырьем» являются ранжировки, построенные по значениям показателей бизнесов (объектов).

П р и м е р (продолжение).

Для, данных приведенных выше, ранги объектов по каждому показателю приведены в таблице (более значимым объектам соответствуют меньшие значения рангов):

Показатели (k)	Бизнесы (объекты) (j)
Планируемая прибыль
Оценка риска
Средняя зарплата

Таким образом, имеется три вектора исходных ранжировок:

,

,

.

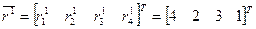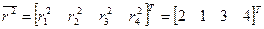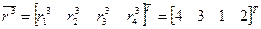Задача заключается в том, чтобы по трём построить одну ранжировку 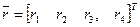, по которой и определить вектор весов .

?

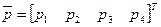Итак, исходными для вычисления вектора весов 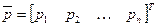является набор векторов ранжировок .

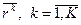Два варианта вычисления вектора весов отличаются тем, что в одном случае используется в качестве меры расстояние Кемени между МПС, а во втором – непосредственно расстояние Кемени между ранжировками. Графически выбор наилучшей ранжировки (по критерию минимума суммы расстояний до ранжировок показателей) условно можно представить так:

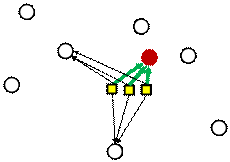
Здесь «квадратики» - ранжировки показателей, «кружки» - остальные возможные ранжировки множества объектов, тонкие стрелки – расстояния до произвольной ранжировки, толстые стрелки – расстояния до оптимальной ранжировки (до которой сумма этих расстояний минимальна.

Дата добавления: 2014-01-04