Вычисление весов по МПС

Автор: Вилисов Валерий Яковлевич, профессор кафедры Математики Технологического университета (г. Королев, Моск. обл.)

В этом алгоритме по каждой ранжировке строится МПС, на основании которых вычисляется вектор весов.

Расстояние Кемени между двумя МПС - 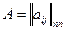и 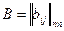, где n – число объектов ранжировки, вычисляется как:

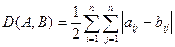. (1)

Медианная мера Кемени (ММК) вычисляется, как сумма расстояний от ранжировки-кандидата_быть_медианой (А) до всех ранжировок-показателей_эффективности_инвестиций ():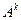

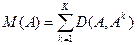. (2)

Здесь K – количество показателей эффективности инвестиций.

Тогда наилучшей является та ранжировка, для которой ММК минимальна, т.е. критерий вычисления медианы Кемени (МК), т.е. медианной ранжировки, имеет вид:

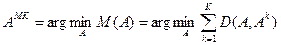. (3)

П р и м е р (продолжение).

Для векторов ранжировок построим МПС ():

,

,

.

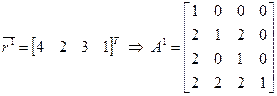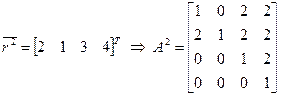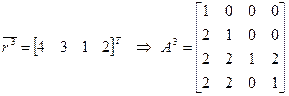В выборе оптимальной ранжировки кроме ранжировок, соответствующих трем показателям эффективности инвестиций, участвуют и другие возможные ранжировки рассматриваемых 4-х объектов. По ним также следует построить их МПС.

Так для некоторой j -й ранжировки:

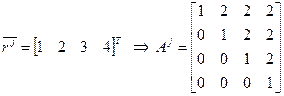
Примечание. Т.к. в (1) имеется сомножитель ½, то для определения расстояния Кемени достаточно вычислить модули сумму модулей разностей лишь, например, верхних треугольников матриц А, а разность диагональных элементов всегда =0. Так:

.

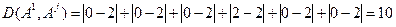Аналогично:

.

.

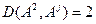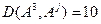Тогда по формуле (2):

.

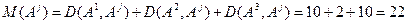Для нахождения МК надо перебрать все возможные ранжировки 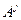и выбрать из них ту, которая имеет минимальную ММК.

МК можно искать среди разных множеств ранжировок, из которых типичны три группы. Для данного примера это следующие:

1. Множество ранжировок показателей (МРП). В данном примере это {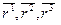} или соответствующие им МПС

{}.

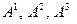2. Всё возможное множество строгих ранжировок (МСР), т.е. таких, в которых каждый объект строго предпочтительнее другого. В это множество входят и ранжировки п.1. Количество возможных ранжировок здесь определяется как число перестановок: 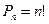, где n – число объектов (бизнесов). Для нашего примера .

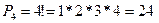3. Полное множество ранжировок (ПМР), которое включает кроме строгих (п.2) и нестрогие (эквивалентность), типа 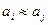. В данном примере полное количество ранжировок составит 69.

Часто для вычисления вектора весов объектов достаточно бывает отыскать МК среди МСР.

При любом из этих трёх вариантов множеств выбор МК выполняется методом полного перебора.

В некоторых случаях можно в качестве грубого приближения определить МК и среди МРП, (т.е. среди себя). Для данных примера найдем МК среди МРП методом полного перебора:

.

.

.

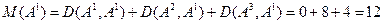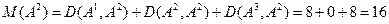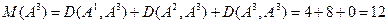Таким образом, здесь на роль МК претендуют две МПС - 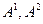и соответствующие им ранжировк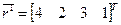и и 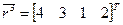. Поскольку в ранжировках наиболее важному объекту соответствует наименьший номер, а в весах существует порядок, обратный ранговому, то для определения весов вычислим соответствующие им обратные ранжировк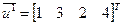и: и .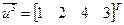

Далее эти обратные ранжировки можно сложить по элементам, и пронормировать (придать смысл вероятностей), тогда:

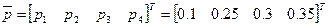
Тогда общий инвестиционный фонд может быть распределен по бизнесам (объектам) пропорционально этим весам.

?

Достоинством алгоритма распределения весов по МПС является полнота анализа – возможность учета всех ранжировок.

Главным недостатком распределения весов по МПС является то, что единственным способом определения итоговой ранжировки является метод полного перебора.

Компромиссным вариантом вычисления весов является следующий алгоритм.

Дата добавления: 2014-01-04