
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вычисление весов непосредственно по ранжировкам
|
|
|
|
Автор: Вилисов Валерий Яковлевич, профессор кафедры Математики Технологического университета (г. Королев, Моск. обл.)
В отличии от предыдущего алгоритма здесь применяется мера расстояния между ранжировками 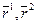 в следующем виде:
в следующем виде:
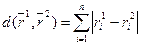 . (4)
. (4)
В данном алгоритме ранжировкам ставится в соответствие сортировка.
В ранжировке – места соответствуют номерам объектов, а значения рангов на этих местах соответствует важности данного объекта.
В сортировке – места соответствуют важности объекта, а значения на этих местах – номеру объекта (на первом месте – самый важный объект).
П р и м е р (продолжение).
Ранжировке 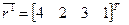 соответствует сортировка
соответствует сортировка 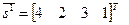 , а
, а 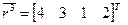 - сортировка
- сортировка 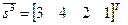 .
.
?
Представление ранжировок сортировками позволяет рассмотреть задачу выбора МК (по ранжировкам, а не МПС), как задачу о назначениях объектов на места в сортировке.
Эта задача также может быть решена полным перебором, однако возможно и аналитическое решение как стандартной оптимизационной задачи о назначениях (транспортная задача с булевыми переменными).
Искомыми переменными здесь являют элементы квадратной матрицы 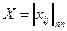 , принимающие булевы значения, где
, принимающие булевы значения, где 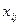 означает, что i –й объект назначается на j –е место в сортировке.
означает, что i –й объект назначается на j –е место в сортировке.
После поиска оптимальной сортировки строится соответствующая ей ранжировка, по которой и вычисляются веса.
Задача о назначениях имеет вид:
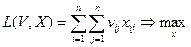 . (5)
. (5)
при ограничениях:
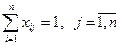 (6)
(6)
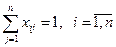 (7)
(7)
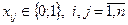 (8)
(8)
Здесь матрица потерь 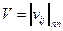 формируется на основе вычисления расстояний Кемени между ранжировками (4) в следующем виде:
формируется на основе вычисления расстояний Кемени между ранжировками (4) в следующем виде:
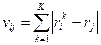 , (9)
, (9)
где 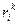 - i -й элемент k –й ранжировки (показателя);
- i -й элемент k –й ранжировки (показателя); 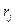 - элемент ранжировки, в которой i –й объект стоит на j –м месте.
- элемент ранжировки, в которой i –й объект стоит на j –м месте.
П р и м е р (продолжение).
?
…
Литература
- Бережная Е.В. Математические методы моделирования экономических систем: Учебное пособие. - М.: Финансы и статистика, 2008.
- Ильченко А.Н. Практикум по экономико-математическим методам: Учебное пособие / А.Н. Ильченко, О.Л. Ксенофонтова, Г.В. Канакина. – М.: Финансы и статистика, 2009.
- Колемаев В.А. Математическая экономика: Учеб. для вузов/ В.А. Колемаев. – М.: ЮНИТИ, 2002.
- Кундышева Е.С. Экономико-математическое моделирование: Учебник. – М.: Дашков и К, 2010.
- Просветов Г.И. Математические методы в экономике: Учебно-методическое пособие. – М.: РДЛ, 2005.
- Экономико-математические методы и прикладные модели. / Под ред. В.В.Федосеева. – М.: ЮНИТИ, 2005.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 456; Нарушение авторских прав?; Мы поможем в написании вашей работы!