Т.к. частота , то

Индуктивности рассеивания обмоток.

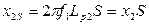, (5)

где – индуктивное сопротивление неподвижного ротора

Уравнение электрического состояния фазы обмотки статора по аналогии с Т.

Для фазы обмотки короткозамкнутого ротора (), будем иметь уравнение:

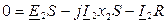или поделив на 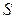, получим

,

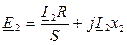. (6)

Уравнению (6) соответствует схема замещения фазы цепи обмотки ротора (рис. 1).

Из уравнения (1) следует уравнение равенства МДС двигателя

, (7)

из которого может быть получено уравнение токов двигателя:

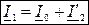, (8)

где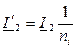– приведенное значение тока ротора;

– коэффициент трансформации тока.

Из (8) следует то, что ток статора содержит две составляющие: составляющую 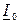= току х.х. и независимую от нагрузки двигателя, т.е. при ; – составляющая, равная компенсационному току , который выполняет ту же роль, что и в Т. и определяется нагрузкой на валу двигателя. Таким образом, любое изменение механической нагрузки двигателя сопровождается соответствующим изменением тока ротора 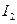, а, следовательно, и тока статора за счет его составляющей 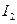. Такое влияние механической нагрузки на ток объясняется тем, что изменение нагрузки вызывает изменение скольжения S. Это в свою очередь согласно (3) влияет на ЭДС ротора, а значит и на его ток, выражение для которого получим из (6)

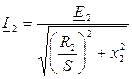или . (9)

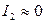Например, в режиме х.х. скольжение ; поэтому ток ротора , а ток статора . В начальный момент ЭДС в нем достигает наибольшее значение 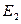и поэтому ток ротора

,

что приводит к значительному увеличению тока статора.

.

2. Энергетические процессы в двигателе

Преобразование активной мощности в двигателе связано с потерями. Эти потери делятся на электрические, магнитные и механические. На рис. Показана энергетическая диаграмма двигателя.

Активная мощность потребляется из сети:

,

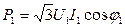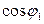– коэффициент мощности двигателя.

Часть этой мощности теряется на нагрев обмотки статора:

Другая часть мощности расходуется на магнитные потери в середине статора:

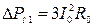
Оставшаяся мощность с помощью основного магнитного потока передается из статора в ротор и представляет собой электромагнитную мощность:

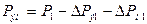или с учетом схемы замещения

, (10)

где – приведенное активное сопротивление ротора.

При этом будем считать, что при любых напряжениях независимо от скольжения активное сопротивление ротора неизменно.

Часть электромагнитной мощности расходуется на нагрев обмотки ротора:

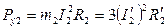или с учетом (10)

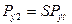, (11)

т.е. мощность электрических потерь в роторе пропорциональна скольжению. Поэтому работа двигателя более экономна при малых скольжениях.

Магнитные потери в сердечнике ротора малы из-за небольшой частоты тока ротора. (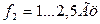), поэтому их не учитывают.

Полная механическая мощность

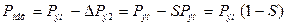, (12)

Мощность 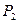, называемая полезной или выходной меньше мощности 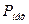на значение механических потерь в роторе, вызванных трением его вала в подшипниках и сопротивлением воздуха:

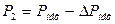, , (13)

поэтому уравнение баланса активной мощности имеет вид:

,

.

На основе Т-образной схемы замещения можно рассмотреть баланс реактивной мощности двигателя. Двигатель потребляет реактивную мощность:

.

Часть этой мощности расходуется на создание поля рассеяния обмотки статора.

Реактивная мощность намагничивания:

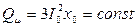расходуется на создание основного магнитного потока и при является неизменной.

Реактивная мощность рассеяния обмотки ротора

.

Таким образом, баланс реактивной мощности определяется уравнением

Основную часть реактивной мощности 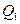составляет мощность , которая из-за наличия воздушного зазора и большого тока намагничивания значительно больше, чем в тр-р (увеличивается магнитное сопротивление на пути основного магнитного потока). Большие значения и существенно влияют на коэффициент мощности и снижают его значение.

При снижении нагрузки 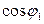значительно уменьшается и при х.х. составляет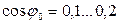

3. Электромагнитные моменты двигателя

Уравнение (13) может быть записано в виде:

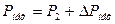
Поделив его правую и левую части на угловую скорость вращения ротора Ω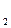получим соответствующее уравнение моментов.

,

где – электромагнитный момент двигателя;

– составляющая электромагнитного момента, уравновешивающая внешний тормозящий момент 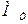, создаваемый рабочим механизмом, т.е. 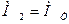. Соответственно 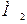называется вращающим моментом.

– составляющая электромагнитного момента, уравновешивающая внутренний тормозной момент , создаваемый силами сопротивления воздуха, а также силами трения вала ротора в подшипниках, т.е.

Так как момент почти не зависит от механической нагрузки, то 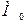часто называют моментом х.х.

В установившемся режиме работы, когда 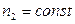, справедливо равенство моментов

,

,

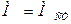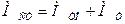где 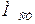– момент статического сопротивления.

Электромагнитный момент создается в результате взаимодействия тока ротора 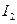с вращающимся магнитным полем и с учетом (12) может быть определен по формуле:

, а ,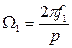

где 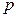– число пар полюсов.

, (14)

Электромагнитная мощность, согласно схеме замещения

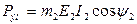(15)

Подставляя (15) в (14) после преобразования получим

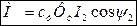(16)

где 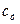– постоянный коэффициент, зависящий от конструкции двигателя.

– угол сдвига фаз между ЭДС и током ротора. Он может быть найден из треугольника сопротивлений, построенного для схемы замещения цепи ротора.

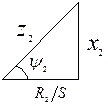
При этом , т.е. этот угол также зависит от скольжения.

Произведение в уравнении (16) есть активная составляющая тока ротора, совпадающая по фазе с ЭДС ротора.

Таким образом, электромагнитный момент двигателя пропорционален магнитному потоку и активной составляющей тока ротора (а не самому току ротора).

На рисунке показана векторная диаграмма ЭДС и токов асинхронного двигателя.

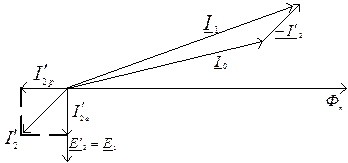Рис. 4.

Для практических расчетов, помимо формулы (16) используется другая формула электромагнитного момента:

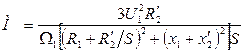(19)

Из (19) следует, что значение электромагнитного момента пропорционально квадрату напряжению сети, т.е. АД чувствителен к изменению этого напряжения. Например: при снижении на 10% электромагнитный момент уменьшается на 19% () и может оказаться недостаточным для приведения в движение рабочего механизма.

Дата добавления: 2014-01-04