
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример 10.6
|
|
|
|
Пример 10.5
Пусть дана леонтьевская балансовая модель “затраты - выпуск” X = AX +Y. Найти вектор конечной продукции Y при заданном X, где
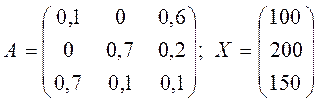 ;
;
Решение. Имеем: Y = (E - A) X, где E - единичная матрица третьего порядка.
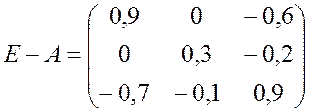 ,
,
значит,
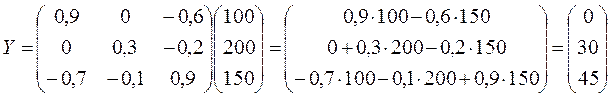
Пусть дана леонтьевская балансовая модель “затраты-выпуск”. Определить, будет ли продуктивной матрица технологических коэффициентов A. Найти вектор валовой продукции X при заданном Y, где
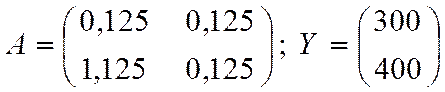 .
.
Решение. Для решения вопроса о продуктивности матрицы A следует найти собственные значения этой матрицы. Составим характеристическое уравнение:
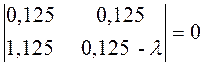 ,
,
или
(0,125 -λ)2 - 0,140625 = (0,125- λ)2-(0,375)2 =(λ+0,25)(λ-0,5)=0
Для заметок
Следовательно, λ 1 = 0,5; λ 2 = - 0,25. Оба корня по модулю меньше единицы, значит, матрица технологических коэффициентов A продуктивная. Для определения вектора валовой продукции X имеем формулу
X = (E - A) -1 Y.
Найдем обратную матрицу для матрицы
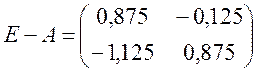 .
.
Обозначим B = E-A, тогда
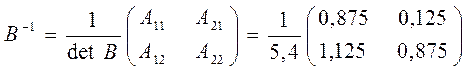 .
.
Следовательно,
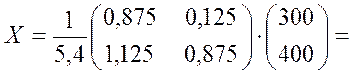
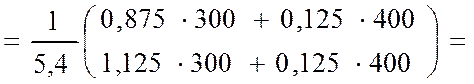
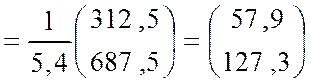
ЛИТЕРАТУРА
1. Ильин В.А., Поздняк Э.Г. Аналитическая геометрия. М. Наука, 1981
2. Общий курс высшей математики для экономистов: Учебник/ Под ред. В.И. Ермакова.-М.: ИНФРА-М, 200. -656 с. _(Высшее образование).
3. Высшая математика для экономистов: Учебн. Пособие для вузов/ Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман; Под ред. Проф. Н.Ш. Кремера. – М.: Банки и биржы, ЮНИТИ, 1997. – 439 с.
4. Сборник задач и упражнений по высшей математике: Общий курс: Учеб. Пособие/ А.В. Кузнецов, Д.С. Кузнецова, Е.И. Шилкина и др.- Мн.: Выш. шк.,1994. – 284 с.: ил.
5. Сборник задач по математике для ВТУЗов. Линейная алгебра и основы математического анализа. /под редакцией Ефимова
6. http://www.mathelp.spb.ru/la/htm
ПРИЛОЖЕНИЯ
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 359; Нарушение авторских прав?; Мы поможем в написании вашей работы!