Первые 10 свойств определителя

1) При транспонировании (замене строк на столбцы и наоборот) определитель не меняется. Для доказательства нужно найти символическую формулу определителя хотя бы 3-го прорядка и, транспонировав, убедиться, что свойство верно:

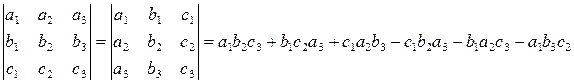
2) При замене строк или столбцов местами определитель меняет знак:

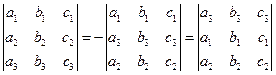(1.3)

Попробуйте сами получить равенства (1.3).

3) Если определитель имеет 2 одинаковые строки или 2 одинаковых столбца (или более), то он равен нулю. Доказательство: используя свойство 2) (меняем одинаковые строки/столбцы местами), получим, что 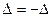, где 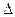есть обозначение определителя. Тогда, перенеся все слагаемые в левую часть, получим: .

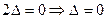4) Постоянный множитель элементов строки/столбца можно вынести за знак определителя:

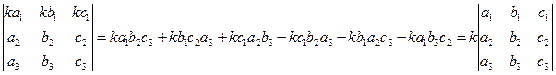(1.4)

5) Если определитель имеет пропорциональные строки/столбцы, то он равен нулю. Доказательство основывается на предыдущих двух свойствах.

6) Если определитель имеет нулевую строку/столбец, то он также равен нулю, учитывая, что нулевая строка/столбец есть произведение любой строки/столбца из определителя и нуля. Получим пропорциональность.

7) Если всякий элемент k-той строки/столбца определителя представляет собой сумму двух слагаемых, то определитель равен сумме 2-х определителей: 1-й имеет в упомянутом k-той строке/столбце 1-ые слагаемое, а второй - вторые. Остальные элементы в определителях не меняются:

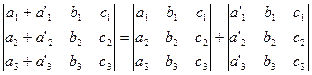(1.5)

Для доказательства (1.5) нужно расписать определитель левой части равенства (1.5) по правилу Саррюса, сгруппировать соответственные суммы и записать получившееся группирование в виде суммы 2-х определителей. Другими словами, доказывается (1.5) «в лоб».

8) Если к любой строке/столбцу определителя прибавить другую строку/столбец, умноженную на произвольное k, то определитель не изменится. Доказательство:

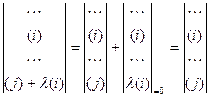(1.6)

где (i) и (j) – строки определителя.

9) Если одна из строк/столбцов определителя является суммой 2-х других строк/столбцов, то определитель равен нулю. Три строки/столбца линейно зависимы,

если для некоторых m и l верно равенство: , где (k), (i) и (j) – строки/столбцы определителя. Это вытекает из следующего свойство.

10) Если определитель имеет линейно зависимые строки/столбцы, то он равен нулю. Доказательство:

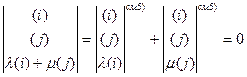(1.7)

Примечание: степень (см. 5)) определителей вовсе не степень, а указание на использование 5-го свойства при доказательстве. В дальнейшем будем именно так указывать подобные ссылки в формулах и выражениях.

Дата добавления: 2014-01-04