Миноры и дополнения

Определение: минором 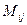является определитель, полученный из данного в результате "вычёркивания" i-той строки и j-того столбца. Например, для определителя 3-го порядка :

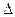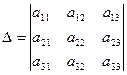
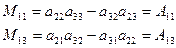
где А₁₁ – алгебраическое дополнение, вычисляемое по общей формуле из минора:

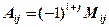(2.1)

Для удобства определения знака алгебраического дополнения (далее АД) можно пользоваться правилом шахматной доски:

,

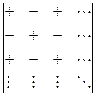где знаки «+» и «–» есть элементы символического «шахматного» определителя, индексы которых соответствуют индексам миноров данного в задаче определителя. Причём знак «+» «шахматного» определителя означает, что знаки у соответствующих миноров и АД совпадают, а знак «–» - различаются.

11) Теорема (11-е свойство): определитель равен сумме произведений элементов некоторой его строки/столбца на их алгебраические дополнения. Например, для определителя (см.выше):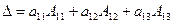

Докажем теорему для определителя 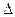, для чего найдём его по правилу Саррюса, вынесем у соответствующей пары слагаемых .

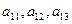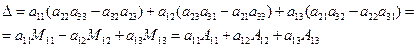
Ч.т.д.

12) Теорема (12-е свойство): сумма произведений элементов некоторой строки/столбца определителя на алгебраические дополнения другой строки/столбца равна нулю.

Доказательство: в заданном определителе на месте j-той строки напишем его i-тую строку. Он станет нулевым (свойство 3). Но АД полученного определителя не изменятся (j-тая строка при нахождении АД «вычёркивалась»). Разложив новый определитель по его новой строке (или столбцу), получим утверждение теоремы, а значит она доказана.

Дата добавления: 2014-01-04