Однородные системы

Исследование систем линейных уравнений

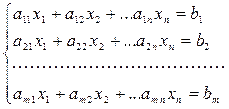(19.1)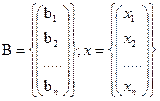

Ее матричная форма записи есть: 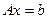(19.2)

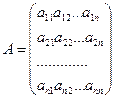
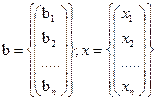
Аx – линейный оператор, переводящий множество столбцов 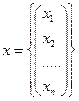в множество столбцов по формуле .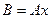

Теорема 19.1:

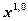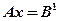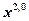Пусть – решение , а – решение 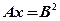, тогда 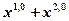- решения.

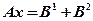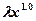, а решение системы .

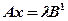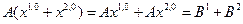
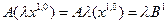
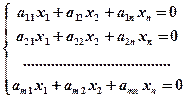(19.7)

Её матричная форма записи:

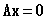(19.8)

Определения:

Система (19.7) - однородная система линейных уравнений.

Система (19.1) - неоднородная система линейных уравнений.

(при 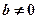, т.е. )

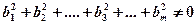Т.е. всякое решение однородной системы (19.8) является ядром линейного оператора. Поэтому множество решений однородной системы (19.8) является линейным пространством.

Теорема 19.2: Множество решений системы (19.7) – линейное пространство размерностью n-r, где r – ранг матрицы А.

Определение: Базисным называется не равный нулю минор матрицы А, порядок которого равняется рангу матрицы.

Определение: Базис во множестве решений однородной системы (19.8) называется фундаментальной системой решений.

Пусть базисный минор содержит столбцы 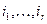. Тогда 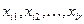– базисные неизвестные, а остальные – свободные неизвестные. Будем считать далее, что неизвестные 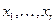– базисные, а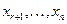– свободные неизвестные.

Положим 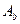– матрица, соответствующая базисному минору у матрицы системы (19.7), а 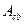– остальные столбцы матрицы этой системы с противоположным знаком. Тогда, перенеся члены со свободными неизвестными в правые части всех уравнений системы (19.7), получим уравнение:

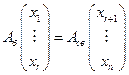(19.9)

А так как матрица в левой части (19.9) - невырожденная, то система (19.9) имеет единственное решение, т.е. каждому набору свободных неизвестных соответствует единственный набор базисных неизвестных.

Доказательство теоремы 19.2:

Рассмотрим наборы:

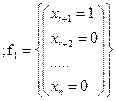
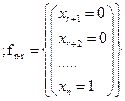(19.10)

Пусть 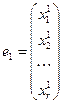– ре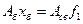шение , – решение 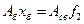, …, 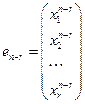– решение системы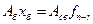

Пусть 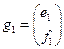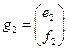… 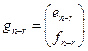(19.12)

Покажем, что 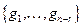– базис в пространстве решений (19.7).

1) Линейная независимость :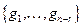

Пусть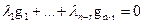, т.е.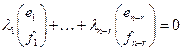

или 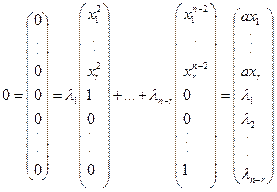(19.13)

Сравнивая в левых и правых частях столбцов равенство (19.7) их нижних n-r чисел, получаем, что 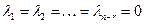, т.е. система 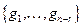– линейно независима.

2) Полнота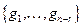

Пусть 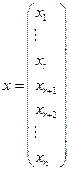– произвольное решение системы (7), тогда имеем 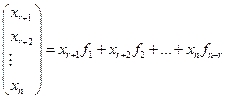(19.14)

(докажите равенство (19.14) используя определение 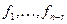в (19.10))

Но согласно формуле (19.9), базисные неизвестные 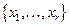однозначно определяются из системы

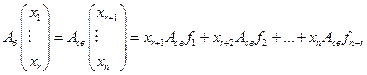(19.15)

поэтому из теоремы 19.1 и равенства (19.15) имеем: 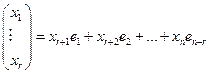(19.16)

Соединяя столбцы в равенство (19.14) и (19.1Б) (сверху напишем столбцы из (19.16), снизу из (19.14)) и используя определение (19.12), получим: 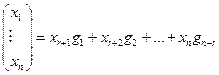(19.17)

Равенство (19.17) означает, что всякое решение системы (19.7) выражается через решения 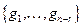по формуле (19.17). Поэтому совокупность решений 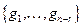– полна, и, сопоставляя с ранее доказанной линейной независимостью 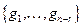, получим, что 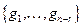– базис, имеющий (n-r) решений. Теорема 19.2 полностью доказана.

Дата добавления: 2014-01-04