Доказательство достаточности теоремы Кронеккер-Капелли

Полагая в системе (19.2): Ax = b все свободные неизвестные нулями, получим систему: 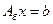(19.18),

где – матрица базисного минора. А так как это матрица невырожденная, то система (19.18) (и система (19.2)) имеет решение.

19.4 Доказательство критерия определённости системы

Если n = r, то по теореме 19.2 множество решений однородной системы (19.7) имеет размерность, равную нулю, то есть решение однородной системы состоит только из одного нулевого решения. Тогда, по теореме 19.3 всякие решения системы (19.1) состоят только из одного частного решения, то есть оно единственно, и поэтому система (19.1) является определённой.

Дата добавления: 2014-01-04