Это фундаментальный закон возрастания точности при росте числа измерений

Ошибка характеризует точность, с которой получено среднее значение измеренной величины . Результат записывается в виде:

. (9)

Эта методика расчета ошибок дает хорошие результаты (с надежностью 0.68) только в том случае, когда одна и та же величина измерялась не менее 30 – 50 раз.

В 1908 году Стьюдент показал, что статистических подход справедлив и при малом числе измерений. Распределение Стьюдента при числе измерений

n → ∞ переходит в распределение Гаусса, а при малом числе отличается от него.

Для расчета абсолютной ошибки при малом количестве измерений вводится специальный коэффициент, зависящий от надежности P и числа измерений n, называемый коэффициентом Стьюдента t.

Опуская теоретические обоснования его введения, заметим, что

Δx = 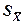·t, (10)

где Δx — абсолютная ошибка для данной доверительной вероятности;
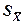— среднеквадратичная ошибка среднего арифметического.

Коэффициенты Стьюдента приведены в таблице 1.

Таблица 1 Коэффициенты Стьюдента
n	Значения Р
0.6	0.8	0.95	0.99	0.999
	1.376	3.078	12.706	63.657	636.61
	1.061	1.886	4.303	9.925	31.598
	0.978	1.638	3.182	5.841	12.941
	0.941	1.533	2.776	4.604	8.610
	0.920	1.476	2.571	4.032	6.859
	0.896	1.415	2.365	3.499	5.405
	0.883	1.383	2.262	3.250	4.781
	0.876	1.363	2.201	3.106	4.437
∞	0.858	1.319	2.069	2.807	3.767

Из сказанного следует:

1. Величина среднеквадратичной ошибки позволяет вычислить вероятность попадания истинного значения измеряемой величины в любой интервал вблизи среднего арифметического.

При n → ∞ 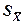→ 0, т.е. интервал, в котором с заданной вероятностью находится истинное значение μ, стремится к нулю с увеличением числа измерений. Казалось бы, увеличивая n, можно получить результат с любой степенью точности. Однако точность существенно увеличивается лишь до тех пор, пока случайная ошибка не станет сравнимой с систематической. Дальнейшее увеличение числа измерений нецелесообразно, т.к. конечная точность результата будет зависеть только от систематической ошибки. Зная величину систематической ошибки, нетрудно задаться допустимой величиной случайной ошибки, взяв ее, например, равной 10% от систематической.

При обработке результатов прямых измерений предлагается следующий порядок операций:

1. Результат каждого измерения запишите в таблицу.

2. Вычислите среднее значение из n измерений .

3. Найдите погрешность отдельного измерения .

Вычислите квадраты погрешностей отдельных измерений (Δ x ₁)², (Δ x ₂)²,..., (Δ x _n)².

4. Определите среднеквадратичную ошибку среднего арифметического

.

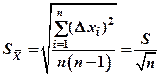5. Задайте значение надежности (обычно берут P = 0.95).

6. Определите коэффициент Стьюдента t для заданной надежности P и числа произведенных измерений n.

7. Найдите доверительный интервал (погрешность измерения) Δ x = 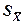· t.

8. Если величина погрешности результата измерения Δx окажется сравнимой с величиной погрешности прибора δ, то в качестве границы доверительного интервала возьмите

.

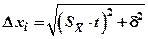Если одна из ошибок меньше другой в три или более раз, то меньшую отбросьте.

9. Окончательный результат запишите в виде .

10. Оцените относительную погрешность результата измерений .

Рассмотрим на числовом примере применение приведенных выше формул.

Пример. Измерялся микрометром диаметр d стержня (систематическая ошибка измерения равна 0.005 мм). Результаты измерений заносим во вторую графу таблицы, находим и в третью графу этой таблицы записываем разности , а в четвертую – их квадраты (таблица 2).

Таблица 2

n	d, мм
	4.02	+ 0.01	0.0001
	3.98	- 0.03	0.0009
	3.97	- 0.04	0.0016
	4.01	+ 0.00	0.0000
	4.05	+ 0.04	0.0016
	4.03	+ 0.02	0.0004
Σ	24.06	–	0.0046

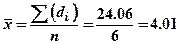мм

мм.

Задавшись надежностью P = 0.95, по таблице коэффициентов Стьюдента для шести измерений найдем t = 2.57. Абсолютная ошибка найдется по формуле (10). Δd = 0.01238 · 2.57 = 0.04 мм.

Сравним случайную и систематическую ошибки: ,

следовательно, δ = 0.005 мм можно отбросить.

Окончательный результат запишем в виде d = (4.01 ± 0.04) мм при Р = 0.95.

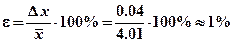
Дата добавления: 2014-01-04