Обработка косвенных измерений

Правила округления

ОКРУГЛЕНИЕ РЕЗУЛЬТАТОВ

Легко видеть, например, что запись a = 2.8674523 ± 0.076 бессмысленна. При ошибке 0.076 последние пять цифр числа не означает ровно ничего.

Если мы допускаем ошибку в сотых долях, то тысячным, тем более десятитысячным долям веры нет. Грамотная запись результата была бы 2.87 ± 0.08. Всегда нужно производить необходимые округления, чтобы не было ложного впечатления о большей, чем это есть на самом деле, точности результатов.

1. Погрешность измерения округляют до первой значащей цифры, всегда увеличивая ее на единицу.
Примеры:

8.27 ≈ 9	0.237 ≈ 0.3
0.0862 ≈ 0.09	0.00035 ≈ 0.0004
857.3 ≈ 900	43.5 ≈ 50

2. Результаты измерения округляют с точностью «до погрешности», т.е. последняя значащая цифра в результате должна находиться в том же разряде, что и в погрешности.

Примеры: 243.871 ± 0.026 ≈ 243.87 ± 0.03; 243.871 ± 2.6 ≈ 244 ± 3; 1053 ± 47 ≈ 1050 ± 50.

3. Округление результата измерения достигается простым отбрасыванием цифр, если первая из отбрасываемых цифр меньше 5.

Примеры: 8.337 (округлить до десятых) ≈ 8.3; 833.438 (округлить до целых) ≈ 833; 0.27375 (округлить до сотых) ≈ 0.27.

4. Если первая из отбрасываемых цифр больше или равна 5, (а за ней одна или несколько цифр отличны от нуля), то последняя из остающихся цифр увеличивается на единицу.

Примеры: 8.3351 (округлить дл сотых) ≈ 8.34; 0.2510 (округлить до десятых) ≈ 0.3; 271.515 (округлить до целых) ≈ 272.

5. Если отбрасываемая цифра равна 5, а за ней нет значащих цифр (или стоят одни нули), то последнюю оставляемую цифру увеличивают на единицу, когда она нечетная, и оставляют неизменной, когда она четная.
Примеры:

0.875 (округлить до сотых) ≈ 0.88; 0.5450 (округлить до сотых) ≈ 0.54; 275.500 (округлить до целых) ≈ 276; 276.500 (округлить до целых) ≈ 276.

Примечание.

a. Значащими называют верные цифры числа, кроме нулей, стоящих впереди числа. Например, 0,00807 – в этом числе имеется три значащих цифры: 8, ноль между 8 и 7 и 7; первые три нуля незначащие. Результаты физических экспериментов записывают только значащими цифрами.
8.12 · 10³ – в этом числе 3 значащих цифры.

b. Записи 15,2 и 15,200 различны. Запись 15,200 означает, что верны сотые и тысячные доли. В записи 15,2 – верны целые и десятые доли.

c. Результаты физических экспериментов записывают только значащими цифрами. Запятую ставят сразу после отличной от нуля цифры, а число умножают на десять в соответствующей степени. Нули, стоящие в начале или конце числа, как правило, не записывают. Например, числа 0,00435 и 234000 записывают так: 4,35∙10^-3 и 2,34·10⁵.

В лабораторной практике большинство измерений — косвенные и интересующая нас величина является функцией одной или нескольких непосредственно измеряемых величин: . (1)

Как следует из теории вероятностей, среднее значение величины определяется подстановкой в формулу (1) средних значений непосредственно измеряемых величин, т.е. ¯. (2)

При проведении косвенных измеренийфункцию F находят для каждого отдельного измерения, а доверительный интервал вычисляют для получения значений искомой величины по тому же методу, что и для прямых измерений.

При обработке результатов косвенных измерений предлагается следующий порядок операций:

Таблица 1 Обработка косвенных измерений
n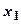
…	...	...	...	...	...
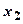
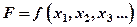
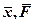
P(надежность) =, t(коэф. Стьюдента) =.
δ(систематическая ошибка = наибольшая ошибка прибора) =
, , , .

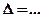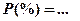1. Выполнить прямые измерения аргументов . Измерения проводить одинаковое число раз n. Полученные результаты занесите в таблицу

2. Вычислить 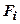. Полученные результаты занесите в таблицу.

3. Далее, для 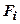примените метод оценки погрешности (ошибки) прямых измерений. Заполните таблицу.

4. Результат измерения запишите в виде:

.

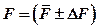5. Определите относительную погрешность результата серии косвенных измерений
.

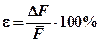Дата добавления: 2014-01-04