Векторы и действия над ними

Вектор – направленный отрезок.

В координатном виде вектор записывается или .

Характеристики вектора:

1. Длина

2. Направление – задается направляющими косинусами

; ; ;

- единичный вектор, имеющий то же направление, что и , .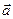

Замечание: Еденичные векторы, сонаправленные с осями координат называются ортами и обозначаются .

Равные вектора – вектора, у которых совпадают и длина и направление.

Нулевой вектор – длина равна нулю, направления нет (точка )

Коллинеарные вектора – вектора, лежащие на одной или параллельных прямых (сонаправлены или противоположно направлены), причем их длина не важна.

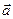и - коллинеарные

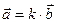k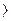0 - векторы сонаправлены

k=1 – векторы равны

- векторы направлены противоположно

Признак коллинеарности:

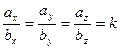
Векторы компланарны – если три и более вектора лежат в одной плоскости.

Действия с векторами

1) Сложение – по правилам треугольника и параллелограмма

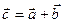
Свойства:

1.

2.

2) Вычитание – по правилам треугольника и параллелограмма

Характерные свойства такие же, как и для обычного вычитания.

3) Умножение на число

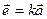
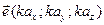
Свойства:

1.

2.

3.

4.

4) Скалярное произведение векторов

Работа есть скалярное произведение вектора силы на вектор перемещения.

Свойства:

1.

2.

3.

Применение скалярного произведения:

1.

2.

3.

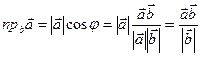
Пример:

;; ;

;

Векторное произведение векторов

Векторное произведение 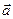на результатом имеет , обладающим следующими свойствами:

1. перпендикулярен плоскости, построенной на 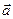и .

2. Направлен так, чтобы поворот был против часовой стрелки.

3. Равен по величине площади параллелограмма, построенном на векторах 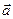и .

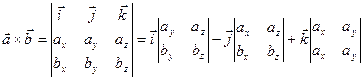
Пример:

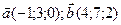
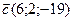
Примечание:

1.

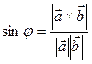
2. Момент силы

3.

Пример:

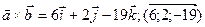
Смешанное произведение векторов

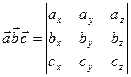
Свойства:

(перемещать только в круговом порядке!)

Примечание:

1. Объем параллелепипеда, построенного на трех векторах, равен модулю смешанного произведения трех векторов.

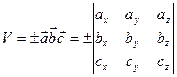
Признак компланарности:

2. Объем пирамиды

Пример:

№1 Проверить будут ли компланарны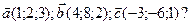

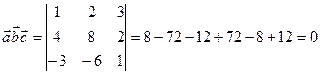
Векторы 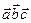- компланарны.

№2 Найти объем пирамиды, построенной на векторах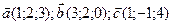

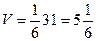
№3 Найти равнодействующую двух сил и работу, которую она совершает по перемещению точки А в точку В.

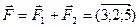
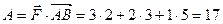
№4 Найти 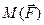, приложенный к точке А относительно точки В.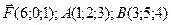

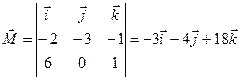
Дата добавления: 2014-01-04