Я лекция. Связь между потенциальной энергией и силой

Работа

РАБОТА И ЭНЕРГИЯ

Я лекция. Законы сохранения

Силы внутренние и внешние. Замкнутая система. Интегралы движения. Сохраняющиеся величины. Связь законов сохранения со свойствами пространства и времени.

Кинетическая энергия. Работа. Мощность. Консервативные и неконсервативные силы. Работа силы тяжести, силы упругости. Работа центральной силы.

Потенциальная энергия частицы во внешнем поле сил. Полная механическая энергия частицы.

Пусть тело, на которое действует сила f, проходит, двигаясь по некоторой траектории, путь s. При этом сила либо изменяет скорость тела, сообщая ему ускорение, либо компенсирует действие другой силы (или сил), противодействующей движению. Действие f на пути s характеризуется величиной, которая называется работой.

Работой называется скалярная величина, равная произведению проекции силы на направление перемещения f _s и пути s, проходимого точкой приложения силы:

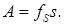
Выражение (24.1) справедливо в том случае, если величина проекции силы f _s на направление перемещения (т. е. на направление скорости) остается все время неизменной. В частности, это имеет место, когда тело движется прямолинейно и постоянная по величине сила f образует с направлением движения постоянный угол α. Поскольку f _s = f cos α, выражению (24.1) можно придать следующий вид:

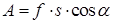
Работа — алгебраическая величина. Если сила и направление перемещения образуют острый угол (cos α >0), работа положительна. Если угол α — тупой (cos α <0), работа отрицательна. При α = π/2 работа равна нулю. Последнее обстоятельство особенно отчетливо показывает, что понятие работы в механике существенно отличается от обыденного представления о работе. В обыденном понимании всякое усилие, в частности мускульное напряжение, всегда сопровождается совершением работы. Например, для того чтобы держать тяжелый груз, стоя неподвижно, а тем более для того, чтобы перенести этот груз по горизонтальному пути, носильщик затрачивает много усилий, т. е. «совершает работу». Однако работа как механическая величина в этих случаях равна нулю.

Если величина проекции силы на направление перемещения не остается постоянной во время движения, для вычисления работы следует разбить путь s на элементарные участки Δ s, взяв их столь малыми, чтобы за время прохождения телом такого участка величину f s можно было считать почти неизменной. Тогда работа силы на каждом элементарном участке приближенно равна

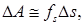
а работа на всем пути s может быть вычислена как сумма элементарных работ:

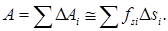
При устремлении всех Δ s, к нулю приближенное равенство (24,3) перейдет в строгое равенство:

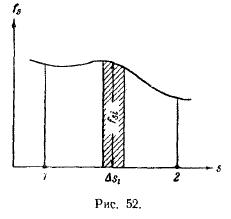
На рис. 52 построен график f _s как функции положения точки на траектории (горизонтальную ось можно назвать осью s, длина отрезка этой оси между точками 1 и 2 равна полной длине пути). Из рисунка видно, что элементарная работа Δ А _i численно равна площади заштрихованной полоски, а работа А на пути от точки 1 до точки 2 численно равна площади фигуры, ограниченной кривой f _s, вертикальными прямыми 1 и 2 и осью s.

Найдем работу, совершаемую при растяжении пружины, подчиняющейся закону Гука. Растяжение будем производить медленно, чтобы силу, с которой мы действуем на пружину, можно было считать все время равной по величине упругой силе f = kx, где х — удлинение пружины. Сила действует в направлении перемещения,

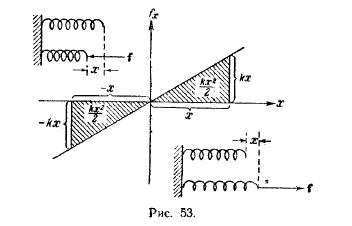
так что f_x — f. Путь, проходимый точкой приложения силы, равен х (рис. 53). Как следует из рис. 53, работа, которую нужно совершить, чтобы вызвать удлинение пружины х, равна

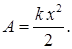
При сжатии пружины на величину х совершается такая же по величине и знаку работа, как и при растяжении. Проекция силы f_x в этом случае отрицательна (сила, действующая на пружину, направлена влево, х растет вправо (см. рис. 53)), все Δ х тоже отрицательны, вследствие чего f_x Δ x положительно.

Отметим, что работа упругой силы, т. е. силы, действующей со стороны пружины на деформирующее ее тело, и при растяжении, и при сжатии равна по величине, но противоположна по направлению силе, вызывающей деформацию.

Единицы работы. В качестве единицы работы служит работа, совершаемая силой, равной единице и действующей в направлении перемещения, на пути, равном единице:

1) в СИ единицей работы является джоуль, который равен работе, совершаемой силой в 1 ньютон на пути в 1 метр;

2) в СГС - системе — эрг, равный работе, совершаемой силой в 1 дину на пути в 1 сантиметр;

3) в МКГСС - системе — килограммометр (кгс - м), равный работе, совершаемой силой в 1 кгс на пути 1 метр.

Между единицами работы имеются соотношения:

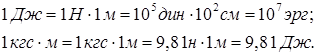
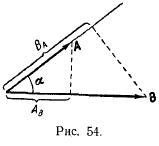
Скалярное произведение векторов. Выражение для работы может быть представлено в виде скалярного произведения вектора силы и вектора перемещения. Скалярным произведением двух векторов А и В называется скаляр, равный произведению модулей этих векторов на косинус угла а между ними (рис. 54).

Символически скалярное произведение записывается в виде АВ, без какого-либо знака между символами векторов.

Итак, скалярное произведение по определению равно

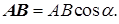
При α остром АВ больше нуля, при α тупом АВ меньше нуля; скалярное произведение двух взаимно-перпендикулярных векторов (α = π/2) равно нулю.

Заметим, что под квадратом вектора подразумевают скалярное произведение вектора на самого себя

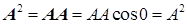
') Ход рассуждений в данном случае точно такой, как и при выводе формулы для пути, пройденного при неравномерном движении (см. § 4).

Условия равновесия механической системы с одной степенью свободы. Потенциальная яма и потенциальный барьер. Финитное и инфинитное движения.

Кинетическая энергия системы частиц. Потенциальная энергия системы частиц во внешнем потенциальном поле. Потенциальная энергия взаимодействия частиц (случай центральных сил).

Дата добавления: 2014-01-04