Условия равновесия механической системы

В замкнутой системе полная энергия остается постоянной, поэтому кинетическая энергия может возрастать только за счет уменьшения потенциальной энергии. Если система находится в таком состоянии, что скорости всех тел равны нулю, а потенциальная энергия имеет минимальное значение, то без воздействия извне тела системы не могут прийти в движение, т. е. система будет находиться в равновесии.

Таким образом, для замкнутой системы равновесной может быть только такая конфигурация тел, которая соответствует минимуму потенциальной энергии системы.

Рассмотрим случай, когда взаимное расположение тел системы может быть определено с помощью только одной величины, например координаты х. В качестве примера можно привести систему Земля — шарик, скользящий без трения по укрепленной неподвижно изогнутой проволоке (рис. 68,а).

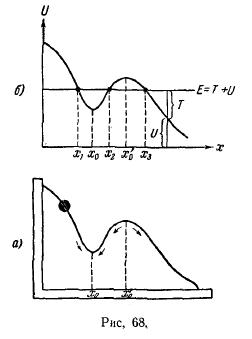
Другим примером может служить прикрепленный к концу пружины шарик, скользящий по горизонтальной направляющей (рис. 69, а). Графики функции U (x) показаны на рис. 68, б и 69, б. Минимумам U соответствуют значения х, равные х 0 (на рис. 69 х 0 есть длина недеформированной пружины). Условие минимума U имеет вид В соответствии с (28. б) условие (29.1) равнозначно тому, что

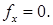
Когда U является функцией только одной переменной х

Таким образом, конфигурация системы, соответствующая минимуму потенциальной энергии, обладает тем свойством, что силы, действующие на тела системы, равны нулю. Этот результат остается справедливым и в общем случае, когда U является функцией нескольких переменных.

В случае, изображенном на рис. 68, условия (29.1) и (29.2) выполняются также для х, равного х '₀ (т. е. для максимума U). Определяемое этим значением х положение шарика также будет равновесным. Однако это равновесие в отличие от равновесия при х = х ₀ будет неустойчивым: достаточно слегка вывести шарик из этого положения, как возникает сила, которая будет удалять шарик от положения х '₀. Силы, возникающие при смещении шарика из положения устойчивого равновесия (для которого х = х ₀), направлены так, что стремятся вернуть шарик в положение равновесия.

Зная вид функции, которой выражается потенциальная энергия системы, можно сделать ряд заключений о характере движения системы. Поясним это, воспользовавшись графиком на рис. 68б. Если полная энергия системы имеет значение, соответствующее проведенной на графике горизонтальной черте, то система может совершать движение либо в пределах от х 1 до х 2 либо в пределах от х 3 до бесконечности. В область х < х 2 и х 2 < х < х 3 система проникнуть не может, так как потенциальная энергия не может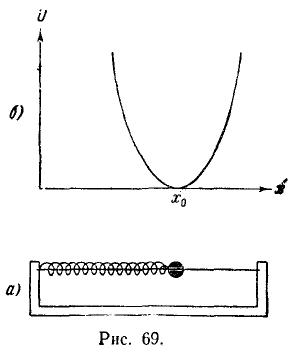

стать больше полной энергии (если бы это случилось, то кинетическая энергия стала бы отрицательной). Таким образом, область х ₂ < х < х ₃ представляет собой потенциальный барьер, через который система не может проникнуть, имея данный запас полной энергии.

Рис. 68, б поясняет, как с помощью графика U определить кинетическую энергию, которой обладает система при данном значении х.

Дата добавления: 2014-01-04