Центральный удар шаров

Я лекция. Соударение двух тел

Абсолютно неупругий удар. Абсолютно упругий центральный удар шаров.

Момент импульса относительно точки и относительно оси. Плечо импульса. Момент силы. Плечо силы. Пара сил. Уравнение для производной момента импульса по времени.

Момент импульса системы материальных точек. Закон сохранения момента импульса. Движение в центральном поле сил (качественно). Космические скорости.

При соударении тел друг с другом они претерпевают деформации. При этом кинетическая энергия, которой обладали тела перед ударом, частично или полностью переходит в потенциальную энергию упругой деформации и в так называемую внутреннюю энергию тел. Увеличение внутренней энергии тел сопровождается повышением их температуры.

Существуют два предельных вида удара: абсолютно упругий и абсолютно неупругий. Абсолютно упругим называется такой удар, при котором механическая энергия тел не переходит в другие, немеханические, виды энергии. При таком ударе кинетическая энергия переходит полностью или частично в потенциальную энергию упругой деформации. Затем тела возвращаются к первоначальной форме, отталкивая друг друга. В итоге потенциальная энергия упругой деформации снова переходит в кинетическую энергию и тела разлетаются со скоростями, величина и направление которых определяются двумя условиями — сохранением полной энергии и сохранением полного импульса системы тел.

Абсолютно неупругий удар характеризуется тем, что потенциальной энергии деформации не возникает; кинетическая энергии тел полностью или частично превращается во внутреннюю энергию; после удара столкнувшиеся тела либо движутся с одинаковой скоростью, либо покоятся. При абсолютно неупругом ударе выполняется лишь закон сохранения импульса, закон же сохранения механической энергии не соблюдается — имеет место закон сохранения суммарной энергии различных видов -

механической и внутренней. Мы ограничимся рассмотрением центрального удара двух шаров. Удар называется центральным если шары до удара движутся вдоль прямой, проходящей через их центры. При центральном

ударе соударение может произойти, если: 1) шары движутся навстречу друг другу (рис. 70, а) и 2) один из шаров догоняет другой (рис. 70, б).

Будем предполагать, что шары образуют замкнутую систему или что внешние силы, приложенные к шарам, уравновешивают друг друга.

Рассмотрим вначале абсолютно неупругий удар. Пусть массы шаров равны m ₁ и m ₂, а скорости до удара v ₁₀ и v ₂₀. В силу закона сохранения суммарный импульс шаров после удара должен быть таким же, как и до удара:

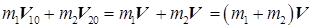
(V — одинаковая для обоих шаров скорость после удара).

Из (30.1) следует, что

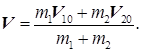
Поскольку векторы v ₁₀ и v ₂₀ направлены вдоль одной и той же прямой, вектор v также имеет направление, совпадающее с этой прямой. В случае б) (см. рис. 70) он направлен в ту же сторону, что и векторы v ₁₀ и v ₂₀. В случае а) вектор v направлен в сторону того из векторов v _i0, для которого произведение m _i v _i0 больше.

Модуль вектора v может быть вычислен по следующей формуле:

где v ₁₀ и v ₂₀ — модули векторов v ₁₀ и v ₂₀; знак «—» соответствует случаю а), знак «+» — случаю б).

Теперь рассмотрим абсолютно упругий удар. При таком ударе выполняются два закона сохранения: закон сохранения импульса и закон сохранения механической энергии.

Обозначим массы шаров m ₁ и m ₂, скорости шаров до удара v ₁₀ и v ₂₀ и, наконец, скорости шаров после удара v ₁ и v ₂. Напишем уравнения сохранения импульса и энергии:

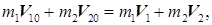
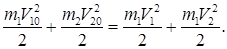
Преобразуем (30.4) следующим образом:

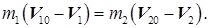
Учитывая, что (А² — В²) = (А— В) (А + В), приведем (30.5) к виду

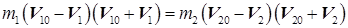
Из соображений симметрии можно утверждать, что скорости шаров после удара будут направлены вдоль той же прямой, вдоль которой двигались центры шаров перед ударом. Следовательно, все векторы в (30.6) и (30.7) коллинеарны. Это дает возможность заключить из сравнения (30.6) и (30.7), что

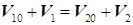
Умножая (30.8) на m₂ и вычитая результат из (30.6), а затем умножая (30.8) на m ₁ и складывая результат с (30.6), получим векторы скоростей шаров после удара:

Для численных подсчетов спроектируем (30.9) на направление вектора v ₁₀:

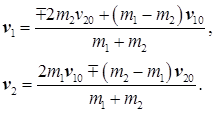
В этих формулах v ₁₀ и v ₂₀ — модули, a v _i и v ₂ — проекции соответствующих векторов. Верхний знак «—» соответствует случаю шаров, движущихся навстречу друг другу, нижний знак «+» — случаю, когда первый шар нагоняет второй.

Отметим, что скорости шаров после абсолютно упругого удара не могут быть одинаковыми. В самом деле, приравняв друг другу выражения (30.9) для v ₁ и v ₂ и произведя преобразования, получим

Следовательно, для того чтобы скорости шаров после удара оказались одинаковыми, необходимо, чтобы они были одинаковыми и до удара, но в этом случае соударение не может произойти. Отсюда следует, что условие равенства скоростей шаров после удара несовместимо с законом сохранения энергии. Итак, при неупругом ударе механическая энергия не сохраняется — она частично переходит во внутреннюю энергию соударяющихся тел, что приводит к их нагреву.

Рассмотрим случай, когда массы соударяющихся шаров равны: m ₁ и m ₂. Из (30.9) следует, что при этом условии

Дата добавления: 2014-01-04