Кинетическая энергия твердого тела

Я лекция. Кинетическая энергия твердого тела

Кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси. Работа, совершаемая внешними силами при вращении твердого тела. Сопоставление формул механики вращательного движения с аналогичными формулами механики поступательного движения.

Динамика плоского движения тела. Угловое ускорение твердого тела при плоском движении. Кинетическая энергия твердого тела при плоском движении.

Законы динамики твердого тела.

Вращение тела вокруг неподвижной оси. Пусть тело вращается вокруг неподвижной оси, которую мы назовем осью z. Линейная скорость элементарной массы Δ m _i может быть представлена в виде

где R _i — расстояние Δ m _i от оси z. Следовательно, кинематическая энергия i -й элементарной массы равна

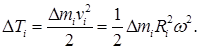
Кинетическая энергия тела слагается из кинетических энергий его частей:

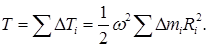
Сумма в правой части этого соотношения представляет собой момент инерции тела I _z относительно оси вращения. Таким образом, кинетическая энергия тела, вращающегося вокруг неподвижной оси, равна

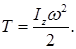
Полученное выражение аналогично выражению для кинетической энергии тела, движущегося поступательно,

При вращательном движении роль массы играет момент инерции, а роль линейной скорости — угловая скорость.

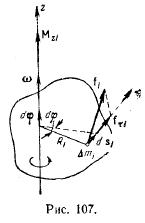
Работа внешних сил при вращении твердого тела. Найдем работу, которую совершают внешние силы при вращении тела вокруг неподвижной оси z. Обозначим внешнюю силу, приложенную к элементарной массе Δ m _i через f _i. За время dt i -я

элементарная масса проходит путь (рис. 107) 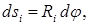где d φ — угол, на который поворачивается тело за время dt. Работа силы fi на этом пути определяется проекцией силы на направление перемещения, которую можно обозначить символом fτi (τ — единичный вектор касательной к окружности, по которой движется i -я элементарная масса; направление этого вектора совпадает с направлением перемещения в данный момент).

Таким образом,

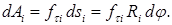
Но f _τi R _i равно модулю момента силы f _i относительно оси z, т. е. | М _zi|, взятому со знаком «+», если f _τi положительна, и со знаком «—», если f _τi отрицательна [см. формулу (36.10); в этой формуле f _τ — не проекция, а модуль силы f _τ]. Следовательно,

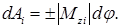
Элементарный угол поворота можно рассматривать как аксиальный вектор

Легко сообразить, что работа dA _i,- будет положительна, когда вектор М _zi,- имеет такое же направление, как и d φ, и отрицательна, если направления векторов М _zi и d φ противоположны. Поэтому формуле (40.2) можно придать вид:

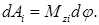
Работа всех сил, приложенных к телу, равна сумме работ, совершаемых отдельными силами:

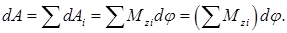
Сумма, стоящая в скобках, дает результирующий момент М _z всех приложенных к телу внешних сил относительно оси вращения. Следовательно,

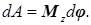
Это выражение аналогично выражению для работы при поступательном движении: dA = f d s. Из сопоставления следует, что в случае вращения роль силы играет момент силы, а роль линейного перемещения d s = v dt — угловое перемещение d φ = ω dt.

Практически для вычисления работы пользуются выражением

где под M _ω подразумевается проекция результирующего момента приложенных к телу внешних сил на направление вектора ω. Работа за конечный промежуток времени находится путем интегрирования выражения (40.4):

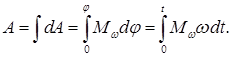
Если проекция результирующего момента сил на направление ω остается постоянной, ее можно вынести за знак интеграла:

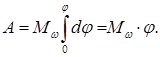
(φ — угол, на который поворачивается тело за время t).

Кинетическая энергия тела при плоском движении.

Плоское движение тела, как мы видели в § 34, может быть представлено как наложение двух движений — поступательного с некоторой скоростью v ₀ и вращения вокруг соответствующей оси.. Свяжем с телом систему координат К ', ось z ' которой направим вдоль вектора угловой скорости вращения тела ω. Согласно формуле (33.13) скорость i '-й элементарной массы тела в неподвижной системе координат К, может быть представлена в виде

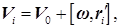
где v ₀ — скорость начала координат О' системы К', r '_i - радиус-вектор, определяющий положение элементарной массы по отношению к точке О'.

Кинетическая энергия i'-й элементарной массы равна

.

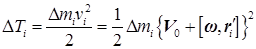Осуществив возведение в квадрат, получим:

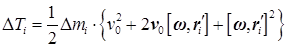
Векторное произведение ω на r '_i можно, как мы знаем, заменить векторным произведением ω на R _i, — • перпендикулярную к оси z' составляющую радиуса-вектора r '_i [см. формулу (11.4) и следующий за ней текст]. Модуль этого векторного произведения равен ω R_i (ω и R _i взаимно перпендикулярны). Следовательно, [ ω, r '_i ]² = ω² R_i ². Подставим это значение в (40.1) и просуммируем Δ T_i - по всем элементарным массам. В результате мы получим кинетическую энергию тела:

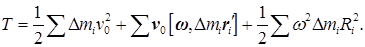
Вынесем всюду постоянные множители за знак суммы:

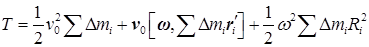
Дата добавления: 2014-01-04