Понятие об общей теории относительности

Я лекция. Релятивистское уравнение динамики частицы

Релятивистское уравнение динамики частицы (второй закон Ньютона). Представление об общей теории относительности. Экспериментальные подтверждения общей теории относительности: красное, гравитационное смещения частоты спектральных линий, прецессия перигелия Меркурия, искривление светового луча в гравитационном поле Солнца.

Созданная А. Эйнштейном в 1916 г. общая теория относительности (ОТО) представляет собой классическую (неквантовую) релятивистскую теорию гравитации. Некоторые физики склонны считать ОТО самой красивой из существующих физических теорий.

В основу ОТО Эйнштейн положил принцип эквивалентности (см. § 7.4), согласно которому свойства движения в неинерциальной системе отсчета те же, что и в инерциальной системе при наличии гравитационного поля. Таким образом, неинерциальная система отсчета эквивалентна некоторому гравитационному полю.

Из принципа эквивалентности вытекает, что все явления, которые обусловлены неинерциальностью системы отсчета, могут наблюдаться в инерциальной системе в результате действия сил тяготения.

В качестве примера рассмотрим движение в вакууме световой частицы — фотона (совокупность таких частиц, летящих «бок о бок», образует световой луч). Из оптики известно, что в вакууме в отсутствие каких-либо полей световые лучи прямолинейны. Следовательно, в инерциальной системе отсчета в отсутствии гравитационного поля

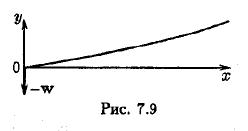
фотон летит со скоростью c по прямолинейной траектории. Примем эту траекторию за ось x (рис.7.9). В неинерциальной системе отсчета, движущейся с ускорением – w параллельно оси y, фотон будет обладать ускорением w, перпендикулярным к оси x.

Поэтому относительно неинерциальной системы отсчета, одновременно с движением вдоль оси x со скоростью с, фотон будет двигаться равноускоренно вдоль оси у. За время t фотон пройдет вдоль оси х путь х = ct и вдоль оси у путь у = wt²/ 2. Исключив из выражений для х и у время t, получим уравнение траектории фотона, т. е. уравнение луча в неинерциальной системе отсчета:

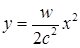
Таким образом, световой луч, прямолинейный в инерциальной системе отсчета, в неинерциальной системе отсчета искривляется и приобретает форму параболы.

Согласно принципу эквивалентности такое же искривление луча должно наблюдаться в инерциальной системе отсчета под действием перпендикулярного к лучу гравитационного поля. Отсюда заключаем, что световые частицы — фотоны подвержены действию сил тяготения.

В § 6.3 мы отмечали, что пространство, в котором квадрат расстояния dl между двумя точками определяется выражением

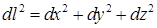
называется евклидовым. В таком пространстве справедлива евклидова геометрия, в которой постулируется, что линии, вдоль которых расстояние между двумя точками минимально, являются прямыми (образно можно сказать, что прямая есть кратчайшее расстояние между двумя точками). В евклидовой геометрии сумма углов треугольника равна π, а отношение длины окружности к радиусу равно 2 π. Пространство с такими свойствами называется плоским.

Псевдоевклидово четырехмерное пространство-время в отсутствие гравитации­онных полей также является плоским. При переходе в неинерциальную систему отсчета пространство-время оказывается искривленным.

Рассмотрим понятие кривизны пространства на примере двумерных пространств. В случае двумерного плоского пространства множество принадлежащих ему точек образует плоскость и кривизна пространства равна нулю. Простейшим двумерным пространством с отличной от нуля кривизной является сфера (рис. 7.10). Кривизна этого пространства растет с уменьшением R и принимается равной 1/ R ².

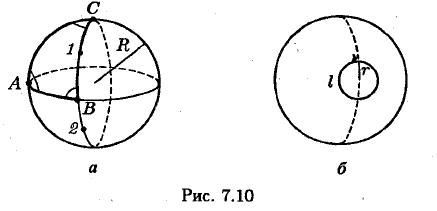
Кратчайшим расстоянием между точками 1 и 2 в таком пространстве является не прямая (точки которой не принадлежат данному пространству), а дуга большой окружности (т. е. окружности, которая делит сферу на две равные части).

Линии, вдоль которых расстояние между двумя точками является минимальным, называются геодезическими. В случае сферы геодезическими линиями являются большие окружности.

Геометрия сферического пространства неевклидова. Это, в частности, проявляется в том, что сумма углов треугольника превышает π (рис. 7.10 а), а длина окружности меньше 2 π R (рис. 7.106).

Действительно, все углы при вершинах треугольника ABC на рис. 7.10 а равны π/2; следовательно, сумма углов равна Зπ/2. Из рис. 7.10 б видно, что равный отрезку дуги большой окружности радиус окружности, построенной в двумерном сферическом пространстве, превышает радиус окружности на плоскости.

Мы выяснили неевклидовость двумерного сферического пространства, рассматривая его «со стороны» из трехмерного пространства. Однако «обитатели» сферы могли бы установить неевклидовость пространства, в котором они «живут», не выходя за его пределы. Для этого им достаточно было бы обнаружить, что сумма углов треугольника отлична от π, а длина окружности не равна 2πR.

Аналогично обстоит дело в случае трехмерного пространства, в котором мы живем. Для того чтобы определить метрику этого пространства, нет необходимости рассматривать его со стороны из четырехмерного пространства (что невозможно). Достаточно, скажем, определить сумму углов треугольника и отношение длины окружности к ее радиусу. Следует иметь в виду, что вблизи поверхности Земли неевклидовость пространства крайне мала и не может наблюдаться непосредственно.

Вся совокупность экспериментальных данных указывает на то, что пространство, в котором мы живем, является практически плоским (т. е. евклидовым) лишь в случае слабых гравитационных полей (к числу которых относится поле Земли). Однако вблизи больших гравитирующих масс это пространство искривляется и становится неевклидовым.

Обратимся к четырехмерному пространству-времени. При наличии гравитационного поля оно оказывается искривленным. Кратчайшим расстоянием между двумя мировыми точками в пространстве-времени является геодезическая линия.

Согласно Эйнштейну никаких специальных гравитационных сил не существует и всякое тело всегда движется в пространстве-времени «свободно» вдоль геодезических линий. При этом в обычном трехмерном пространстве тело движется, вообще говоря, вдоль криволинейных траекторий с переменной скоростью, т. е. так, как оно двигалось бы под действием некоторой силы.

Дата добавления: 2014-01-04