Поняття функції. Способи завдання числових функцій

Означення. Нехай і – дві не порожні множини. Якщо кожному елементу за певним законом поставлено у відповідність єдиний елемент 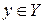, то кажуть, що задано відображення множини у множину , або функція, яка визначена на множині і приймає значення із множини .

Це записують, наприклад, так:

, або , або .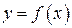

Тут літерою 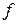(або якою-небудь іншою) позначено той закон чи правило, за яким встановлюється відповідність між х і у. Елемент х називається прообразом, а елемент у – його образом. Множина називається областю визначення функції, а множина – областю значень функції.

Серед способів завдання числових функцій в математичному аналізі найбільш уживаним є аналітичний спосіб, коли функція визначається аналітичним виразом (формулою). Цей вираз вказує, які дії слід виконати над даним значенням аргументу, щоб одержати відповідне значення функції, наприклад: , . Якщо при цьому область визначення функції не вказується, то під нею розуміється область існування аналітичного виразу, тобто множина всіх дійсних значень аргументу, для яких аналітичний вираз має зміст („область припустимих значень”).

Досить часто користуються графічним способом завдання функції. Графіком функції 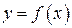називається множина точок площини, які мають координати . Отже, якщо задано графік функції, то цим встановлено відповідність між абсцисами х (значенням незалежної змінної) і ординатами 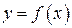(відповідними значеннями функції). Графічно визначені функції пов’язані, зокрема, з наслідками роботи самописних приладів, таких як осцилограф (реєстрація змін електричного струму або напруги), барограф (реєстрація змін атмосферного тичку), електрокардіограф і т.п. Графіки, виписані цими приладами задають функції, властивості яких описують перебіг відповідних процесів. В математиці часто виявляється доцільним користуватися графіками аналітично заданих функцій для їх геометричного зображення і унаочнення їх властивостей.

При табличному способі завдання функції обирається певна множина значень аргументу і для кожного з них указується відповідне значення функції :

х	x 1	x 2	…	xn
y = f (x)	f (x 1)	f (x 2)	…	f (xn)

Табличне завдання функції випливає зокрема як наслідок експерименту, в якому незалежній змінній експериментатор надає певні значення і вимірює відповідні значення функції. Таблиці складають і для функцій, які задані аналітично і часто використовуються, коли безпосереднє обчислення їх значень пов’язане з труднощами (таблиці тригонометричних функцій, логарифмів, тощо). Звичайно, таблиця не може подати всі значення функції. Ті значення функції, які відповідають проміжним значенням аргументу, не включеним до таблиці, можна знайти лише наближено, шляхом інтерполяції.

Сучасне широке поширення електронних обчислювальних пристроїв, від мікрокалькулятора і до суперкомп’ютера, зробило одним із найважливіших способів завдання функції програмний спосіб, коли функцію визначають програмою, за якою обчислювальний пристрій для заданого значення аргументу знаходить відповідне значення функції.

Ми розглянули найбільш уживані способи визначення функцій, але взагалі цих способів може бути безліч, аж до простого словесного опису залежності між змінними.

Приклад. Так звана функція Діріхле задана на множині дійсних чисел, кожному раціональному числу ставить у відповідність число 1, а ірраціональному числу – число 0:

Цим описом функція Діріхле цілком визначена, а от завдати її одним з перелічених вище способів практично неможливо.

Над функціями визначаються арифметичні дії. Нехай функція визначена на множині , а функція визначена на множині , при чому переріз

.

Тоді на множині Х визначена сума функцій 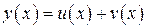, так що

.

Цілком аналогічно визначаються різниця , добуток та частка (частка визначена в тих точках множини Х, в яких ).

Якщо функція визначена на множині і відображає її у множину , а на множині Х визначена функція , яка відображає множину Х у множину , то кожному відповідає , а кожному відповідає певне значення . В решті решт ми отримуємо відображення множини Х у множину , яке позначається і називається складеною функцією від х, або композицією функцій та , або функцією від функції. При цьому називають проміжним аргументом або внутрішньою функцією, а – зовнішньою функцією. Так, наприклад, є композицією двох функцій , і , . Ця композиція відображає множину у множину .

Дата добавления: 2014-01-04