Класифікація функцій. Поняття елементарної функції

Основними елементарними функціями називаються:

1. Стала функція ;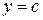

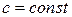2. Степенева функція 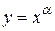, aÎ R;

3. Показникова функція ;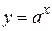

4. Логарифмічна функція ;

5. Тригонометричні функції: , , ;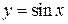

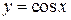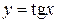6. Обернені тригонометричні функції: , , .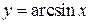

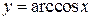Функція, визначена одним аналітичним виразом (формулою), утвореним з основних елементарних функцій за допомогою скінченного числа арифметичних дій і композицій (утворення складених функцій) називається елементарною. Наприклад, 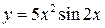, , 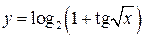тощо.

Всі інші функції називаються неелементарними. Зокрема, неелементарною є функція, задана різними аналітичними виразами для різних інтервалів зміни аргументу, наприклад

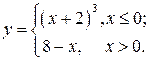
Елементарні функції поділяються на кілька класів.

1. Функція вигляду

,

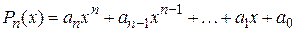де п Î N, 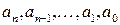– будь-які числа 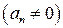називається цілою раціональною функцією або многочленом (поліномом) степеня п. Многочлен першого степеня називають також лінійною функцією, а многочлен другого степеня – квадратичною функцією.

2. Функція, що являє собою відношення двох многочленів

,

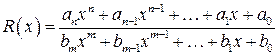називається дробово-раціональною функцією, Многочлен і дробово-раціональні функції разом утворюють клас раціональних функцій.

3. Функція, яка отримана за допомогою скінченного числа арифметичних дій і композицій над степеневими функціями з раціональними показниками, і не є раціональною, називається ірраціональною функцією, наприклад , .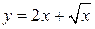

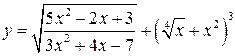Раціональні і ірраціональні функції входять до більш загального класу – алгебраїчних функцій, які визначаються рівнянням виду

,

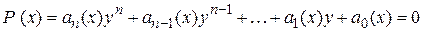де 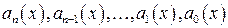є многочленами.

4. Усяка функція, яка не є алгебраїчною, називається трансцендентною. Це, наприклад, функції 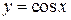, , 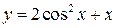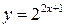і т.д.

4.5. Неявна функція, обернена функція,

Дата добавления: 2014-01-04