Визначні границі

1. Перша визначна границя – це границя

. (4.5)

Доведення. Зауважимо, що при обчисленні цієї границі не можна скористатись властивістю 4 в) границь, тому що границя знаменника дорівнює нулю.

Рис. 4. 3

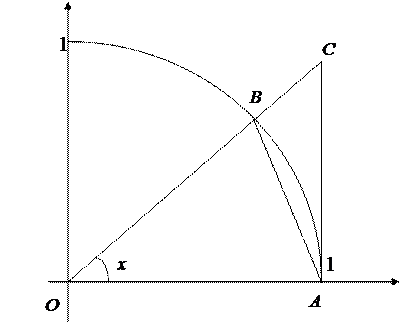В колі одиничного радіуса (рис. 4.3) розглянемо центральний гострий кут х = Ð АОВ, х Î (0; ]. Знайдемо площі трикутників D АОВ і D АОС та сектора АОВ.

S _{D AOB} = ;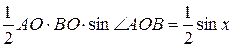

S _{D AOC} = ;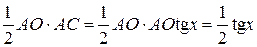

S _{сектора AOB} = .

За малюнком S _{D AOB} < S _{сектора AOB} < S _{D AOC}, отже

.

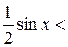
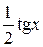Оскільки sin x > 0 при x Î (0; ], можемо розділити ці нерівності почленно на . Одержимо або

.

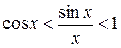Через парність функцій і ці нерівності зберігаються і при x Î (–; 0). При цьому і за властивістю 6 виходить, що .

Наслідки. 1. ;

2. ;

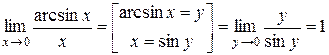3. .

Таким чином, згідно з означенням еквівалентних функцій (4.2), при x ® 0

sin x ~ x;

tg x ~ x;

arcsin x ~ x;

arctg x ~ x.

Очевидно, що всі ці співвідношення залишаться в силі, якщо замінити в них x на яку-небудь нескінченно малу функцію.

Приклад. Обчислити .

= = = = .

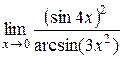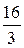2. Друга визначна границя:

, (4.6)

де е» 2, 718 – стала Ейлера.

Наслідок. Нехай a (x) – нескінченно мала функція, а b (x) – нескінченно велика при x ® x ₀. Тоді

. (4.7)

Доведення. Зрозуміло, що рівність (4.6) збережеться, якщо замінити x на будь-яку нескінченно велику функцію. Зробимо деякі арифметичні перетворення:

.

Оскільки a (x) – нескінченно мала функція, то 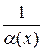– нескінченно велика при x ® x ₀. Таким чином, ® е при x ® x ₀. Звідси і виходить рівність (4.7).

Приклад. Обчислити .

Розв'язання. Тут згідно з еквівалентністю (4.3) , а покажчик степеня нескінченно великий при x ® ¥, тобто маємо невизначеність типу . Саме такого характеру невизначеність у виразі (4.6). Щоб скористатись наслідком (4.7), перетворимо заданий вираз, виділивши в дужках одиницю:

= = = = = = = .

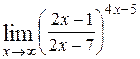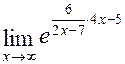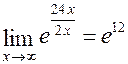Дата добавления: 2014-01-04