Циліндричні поверхні. Циліндри другого порядку

Означення. Циліндричною поверхнею або циліндром називається поверхня, утворена паралельними прямими, які називаються її твірними. Якщо яка-небудь площина перетинає всі твірні циліндра, то лінія перетину (l) називається напрямною цієї циліндричної поверхні (рис. 3.26).

Розглянемо, наприклад, циліндричну поверхню (S) з твірними, паралельними осі О z (рис. 3.26). Нехай (l) – лінія перетину циліндра з площиною О xy, тобто напрямна циліндра. В площині О xy лінія (l) визначиться деяким рівнянням вигляду

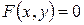. (3.65)

Покажемо, що в просторі це рівняння визначає дану циліндричну поверхню (S). Справді, точка простору лежить на заданому циліндрі тоді и тільки тоді, коли її проекція 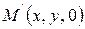на площину О xy лежить на лінії (l), тобто коли її координати x і y задовольняють рівнянням (3.65) незалежно від третьої координати z.

Таким чином, рівняння циліндричної поверхні з твірними, паралельними осі О z, не містить координати z і є ідентичним за формою рівнянню напрямної в площині О xy.

Аналогічно рівняння 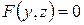і 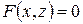визначають циліндричні поверхні, твірні яких паралельні відповідно О x і О y.

Розглянемо найбільш загальний вигляд рівняння поверхні другого порядку, яке не містить змінної z:

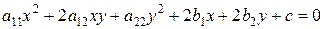(3.66)

Це рівняння визначає циліндричну поверхню з твірними, паралельними осі О z. На площині ж воно визначає алгебраїчну лінію другого порядку, яка являє собою напрямну цього циліндра. Це рівняння було досліджене в п. 3.10. Якщо не враховувати випадків виродження, воно може визначати на площині О xy еліпс, гіперболу, або параболу. Відповідно рівняння (3.66) визначає в просторі еліптичний циліндр (рис. 3.27), гіперболічний циліндр (рис. 3.28) або параболічний циліндр (рис. 3.29).

Дата добавления: 2014-01-04