Матриці, визначники та їх властивості

Передмова

Цей методичний посібник складено у відповідності з діючою програмою для студентів спеціальності «Архітектура» І курсу, І семестру.

Посібник має 4 розділи, які позначені у змісті, в них міститься увесь теоретичний матеріал та наведено багато прикладів розв‘язання різних типів задач.

Рекомендована література

1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 1987. – 320 с.

2. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. – М.: Наука, 1986. – 544 с.

3. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. – М.: Наука, 1983. – 228 с.

4. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. – М.: Наука, 1988. – 431 с.

5. Дубовик В.П., Юрик І.І. Вища математика: Навч. посібник. – К.: Видавництво А.С.К., 2004. – 648 с.

6. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. – М.: Наука, 1988. – 224 с.

7. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: Наука, 1989. – 656 с.

8. Мантуров О.В., Матвеев Н.М. Курс высшей математики. – М.: Высш. шк., 1986. – 399 с.

9. Овчинников П.П., Яремчук Ф.П., Михайленко В.М. Вища математика: Підручник. У 2 ч. – К.: Техніка, 1999. – Ч. 1. - 592 с.

10. Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов: В 3 т. – М.: Наука, 1985. – Т. 1. – 432 с.

11. Шкіль М.І., Колесник Т.В. Вища математика. – К.: Вища шк. Головне вид-во, 1986. – 512 с.

Розділ 1. Матриці і системи лінійних алгебраїчних рівнянь (СЛАР)

Означення. Матрицею розміром 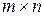називається прямокутна таблиця, складена з 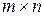чисел, розташованих у 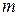рядків і 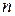стовпців. Ці числа називаються елементами матриці. Якщо 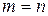, матрицю називають квадратною матрицею порядку 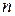. В цьому розділі розглядатимемо лише квадратні матриці.

Матриці позначають великими латинськими літерами, а їх елементи – такими ж малими літерами з подвійними індексами, де перший індекс означає номер рядка, а другий – номер стовпця, на перетині яких стоїть цей елемент. Наприклад, квадратна матриця А третього порядку позначається так:

.

Кажуть, що елементи 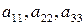утворюють головну діагональ матриці, елементи 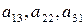– побічну діагональ.

Кожній квадратній матриці ставиться у відповідність число, яке називається визначником або детермінантом цієї матриці. Визначник позначається через , визначник матриці А через 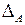чи , а записується подібно до самої матриці, лише замість круглих дужок по боках таблиці елементів ставляться прямолінійні:

.

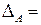
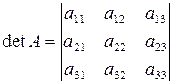Розглянемо правила обчислення визначників. Визначник матриці другого порядку обчислюється за формулою

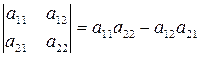(1.1)

(добуток елементів головної діагоналі мінус добуток елементів побічної).

Визначник матриці третього порядку обчислюється за формулою

. (1.2)

Далі визначники другого порядку розкриваються за формулою (1.1), і ми одержуємо вираз визначника через його елементи.

Приклад. Обчислити визначник .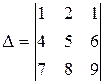

За формулою (1.2):

==

=

=.

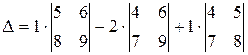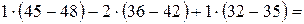
Означення. Мінором елемента 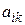даного визначника називається визначник, одержаний з даного визначника викреслюванням і -го рядка і k -го стовпця. Таким чином мінор має порядок на одиницю менший, ніж порядок даного визначника.

Означення. Алгебраїчним доповненням елемента 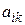називається його мінор, узятий зі своїм знаком, якщо – парне число, і з протилежним знаком, якщо – непарне число, тобто

.

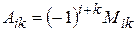Тепер ми бачимо, що формулу (1.2) можна записати у вигляді

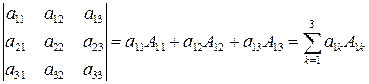. (1.3)

Цю формулу називають розкладанням визначника за елементами першого рядка.

Обчислення визначника будь-якого порядку п виконується за аналогічною формулою:

, (1.4)

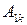таким чином визначник п -го порядку виражається через визначники -го порядку, якими є . Застосовуючи формулу (1.4) до 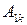і повторюючи цю процедуру, прийдемо кінець кінцем до визначників 2 порядку.

Зауваження. Далі буде з’ясовано, що обчислення будь-якого визначника можна виконувати розкладанням його за елементами не лише першого, але і будь-якого іншого рядка або стовпця.

Приклад. Обчислити визначник

.

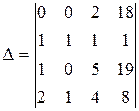Розкладемо визначник за елементами першого рядка відповідно до формули (1.4):

=

== =+

+=.

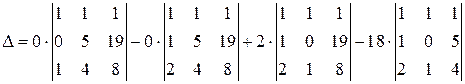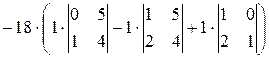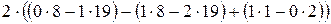
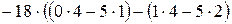Перевіримо слушність зробленого зауваження: розкладемо тепер визначник за елементами другого стовпця:

=

==

=.

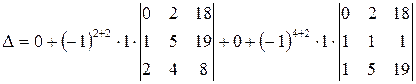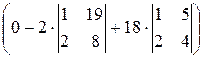
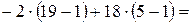
Одержано, як і слід було чекати, той самий результат.

Дата добавления: 2014-01-04