Метод Гаусса розв’язання СЛАР

Якщо коефіцієнти СЛАР є наближеними числами й, особливо, якщо число рівнянь велике, то розв’язання за матричним способом стає занадто трудомістким, а якщо матриця системи вироджена, або якщо система не є квадратною, то взагалі неможливим. Більш економним з точки зору обсягу обчислювальної роботи і більш універсальним способом розв’язання СЛАР є метод Гаусса*). Цей метод полягає в послідовному виключенні невідомих з рівнянь системи за допомогою елементарних перетворень:

1) перестановки двох рівнянь системи;

2) множення обох частин рівняння на одне й те саме число;

3) додавання до обох частин одного рівняння відповідних час­тин іншого рівняння, помножених на деяке число.

Розглянемо застосування метода Гаусса для системи (1.11):

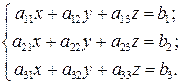(1.11)

Для виключення х із другого рівняння додамо до нього перше, помножене на . Далі, помноживши перше рівняння на і додавши результат до третього рівняння, також виключимо з нього х. Одержимо еквівалентну (1.11) систему рівнянь виду

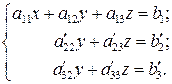(1.15)

де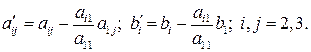

Тепер з третього рівняння системи (1.15) треба виключити у. Для цього помножимо друге рівняння на і додамо результат до третього рівняння. Одержимо

(1.16)

де

Таким чином задану систему приведено, як кажуть, до трикутного вигляду. На цьому завершується прямий хід метода Гаусса. Зазначимо, що в процесі виключення невідомих доводиться виконувати ділення на коефіцієнти 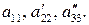Тому вони повинні бути відмінними від нуля; в противному разі необхідно відповідним чином переставити рівняння системи.

Зворотний хід починається з розв’язання третього рівняння системи (1.16):

.

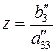Використовуючи це значення, можна знайти у з другого рівняння, а потім х з першого:

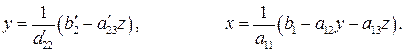(1.17)

Цим і завершується розв’язання системи (1.16).

Цілком аналогічно будується обчислювальний алгоритм для СЛАР з будь-яким числом рівнянь.

Метод Гаусса зручно використовувати, працюючи замість рівнянь з так званою розширеною матрицею системи, яку отримують, приєднуючи до основної матриці системи стовпець правих частин. Наприклад, для системи 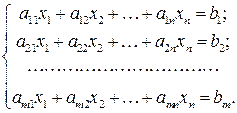(1.9):

(1.9)

розширена матриця системи буде мати вигляд:

.

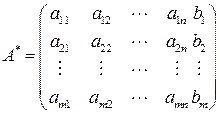З рядками цієї матриці можна виконувати ті ж дії, що і з рівняннями системи, а саме:

1) перестановку двох рядків матриці;

2) множення всіх елементів рядка на одне й те саме число;

3) додавання до елементів одного рядка відповідних елементів іншого рядка, помножених на деяке число. За допомогою цих дій треба привести розширену матрицю системи до трикутного або східчастого вигляду (прямий хід метода Гаусса), а потім, записуючи рівняння, що відповідають рядкам отриманої матриці, виконати зворотній хід.

Зауваження. Якщо виявиться, що в рядку розширеної матриці, зведеної до східчастого вигляду, всі елементи, крім останнього (правої частини), дорівнюють нулю, то відповідне рівняння має вигляд 0· x ₁+0· x ₂+…+0· x_n = b_m ≠0, тобто не має розв’язків, отже система (1.9) несумісна. Якщо ж всі елементи рядка дорівнюють нулю, то відповідне рівняння є тотожністю 0=0 і не містить інформації.

Якщо СЛАР містить більше невідомих, ніж рівнянь, то вона не має однозначного розв’язку. Тоді одні з невідомих виражають через інші, які називають вільними. В усіх рівняннях системи вільні невідомі переносять в праву частину і виконують зворотній хід метода Гаусса. Таким чином отримують розв’язок системи, який містить вільні невідомі.

Приклад 1. Розв’язати систему

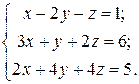
Цю систему вже було розв’язано в попередньому пункті матричним способом. Застосуємо до неї метод Гаусса. Запишемо розширену матрицю системи:

.

Стовпець правих частин зручно відділяти від матриці системи вертикальною рискою. Зведемо цю матрицю до східчастого вигляду. Для цього спочатку до другого рядка додамо перший, помножений на -3, а до третього рядка додамо перший, помножений на -2. Отримаємо матрицю

В результаті другий і третій рядки починаються з нуля. Щоб отримати матрицю східчастого вигляду, потрібно, щоб другий елемент третього рядка також дорівнював нулю. Для цього третій рядок помножимо на 7 і додамо до нього другий рядок, помножений на -8:

.

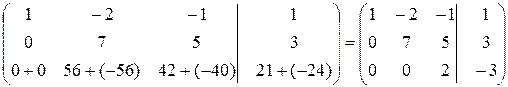Ми виконали прямий хід метода Гаусса. Щоб виконати зворотній хід, запишемо рівняння, що відповідає останньому рядку матриці і розв’яжемо його:

0· х +0· у +2· z = -3, звідси z = -1,5.

Тепер запишемо рівняння, що відповідає другому рядку матриці, замість підставимо знайдене значення і знайдемо у:

0· х +7· у +5· z = 3,

7 у +5·(-1,5) = 3, звідси у = 1,5.

Нарешті, запишемо рівняння, що відповідає першому рядку матриці:

1· х +(-2)· у +(-1)· z = 1,

х +(-2)·1,5+(-1)·(-1,5) = 1, звідси х = 2,5.

Ми знайшли розв’язок х =2,5, у = 1,5, z = -1,5, що співпадає зі знайденим раніше.

Приклад 2. Розв’язати систему

Запишемо розширену матрицю системи:

.

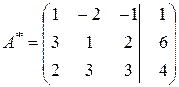Зведемо цю матрицю до східчастого вигляду. Для цього до другого рядка додамо перший, помножений на -3, а до третього рядка додамо перший, помножений на -2. Отримаємо матрицю

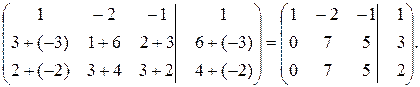
Щоб отримати матрицю східчастого вигляду, потрібно, щоб другий елемент третього рядка також дорівнював нулю. Для цього від третього рядка віднімемо другий:

.

Рівняння, що відповідає останньому рядку матриці, має вигляд:

0· х +0· у +0· z = -1.

Таке рівняння не має розв’язків, отже система несумісна.

Приклад 3. Розв’язати систему

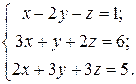
Запишемо розширену матрицю системи:

.

Зведемо цю матрицю до східчастого вигляду. Для цього до другого рядка додамо перший, помножений на -3, а до третього рядка додамо перший, помножений на -2. Отримаємо матрицю

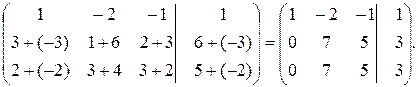
Щоб отримати матрицю східчастого вигляду, потрібно, щоб другий елемент третього рядка також дорівнював нулю. Для цього від третього рядка віднімемо другий:

.

Рівняння, що відповідає останньому рядку матриці, має вигляд:

0· х +0· у +0· z = 0 і не містить інформації.

Запишемо рівняння, що відповідає другому рядку матриці:

0· х +7· у +5· z = 3.

В цьому рівнянні дві невідомі,отже виразимо у через z:

, тобто невідома z буде вільною.

Запишемо рівняння, що відповідає першому рядку матриці, і підставимо в нього знайдене значення у:

1· х +(-2)· у +(-1)· z = 1,

х +(-2)·+(-1)· z = 1,

х = 1+2·+ z,

х = .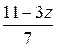

Розв’язком системи будуть будь-які числа х, у та z, для яких виконуються співвідношення: х = 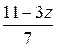, . Таким чином, система має безліч розв’язків.

Дата добавления: 2014-01-04