Лінійними діями над вектораминазиваютьсядодавання (і пов’язане з ним віднімання) векторів і множення вектора на число (скаляр)

Лінійні дії над векторами

Сумою векторів і є вектор, який іде з початку вектора в кінець вектора при умові, що вектор відкладений від кінця вектора (рис 2.1). Це так зване „правило трикутника”.

Іншим способом побудови суми двох векторів є так зване „правило паралелограма”: якщо вектори і відкладені від спільного початку О

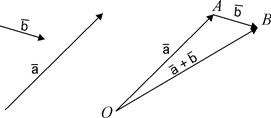
Рис. 2. 1 Рис. 2. 2

(рис. 2.2) і на них побудовано паралелограм, то сума + є вектор , який виходить з того ж початку і суміщається з діагоналлю паралелограма. Зауважимо, що обидва правила дають один і той же результат. Справді, на рис. 2.2 маємо = , = , отже = += + за „правилом трикутника”, так само, як і за „правилом паралелограма”.

„Правило трикутника” легко узагальнюється на випадок суми трьох або більше векторів: від кінця першого вектора відкладаємо другий, від кінця другого – третій і т.д. Сумою всіх цих векторів є вектор, який іде з початку першого вектора в кінець останнього (рис. 2.3). Це так зване „правило многокутника”.

Рис. 2. 3

Дія додавання векторів:

1) комутативна, тобто + = + (див. рис. 2.2);

2) асоціативна, тобто (+ ) + = + (+ ) (див. рис. 2.3), як і додавання чисел.

Різницею векторів – є сума вектора і вектора, протилежного вектору , тобто

– = +(–).

На рис. 2.2 різниця – зображується другою діагоналлю паралелограма ОАВС. Справді +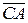= , тобто +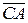= , звідки = – .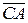

Множення вектора на число. Добутком вектора на число λ називається вектор, який позначається або 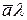і визначається такими умовами:

1) =;

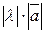2)

Інакше кажучи: якщо λ > 0, то – це вектор, який одержуємо із розтягом в λ разів без зміни напряму; якщо λ < 0, то потрібно розтягнути в | λ | разів і, крім того, змінити напрям на протилежний.

Добуток вектора на число має такі властивості:

1) λ (μ )= (λμ)– асоціативність відносно числових множників;

2) (λ + μ)= λ + μ – дистрибутивність відносно числового множника;

3) λ ()= λ + λ 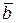– дистрибутивність відносно векторного множника;

4) =для будь-якого числа λ;

5) =для будь-якого вектора ;

6) = ; = –для будь-якого вектора .

Зазначимо, що будь-який вектор можна подати у вигляді 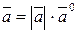, де – орт вектора , тобто вектор одиничної довжини, напрям якого збігається з напрямом вектора .

Сформульовані властивості лінійних дій над векторами цілком аналогічні властивостям відповідних дій над числами, отже дозволяють при лінійних діях з векторами виконувати різні перетворення (розкриття дужок, винесення спільних множників, приведення подібних членів, тощо) так само, як із числами.

Дата добавления: 2014-01-04