Закон Біо-Савара-Лапласа. Магнітне поле прямолінійного та колового струмів

В 1820 році французькі вчені Х.Біо та Ф.Савар експериментально дослідили магнітні поля струмів, що течуть по провідниках різних конфігурацій (прямолінійний, коловий, соленоїд тощо). Узагальнюючи їх експериментальні результати, Лаплас сформулював диференціальний закон, що дістав назву закону Біо-Савара-Лапласа:

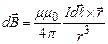(4.9)

або в скалярній формі:

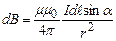. (4.10)

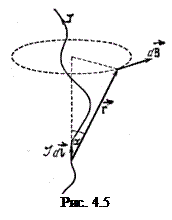
Цей закон визначає індукцію магнітного поля, створеного елементом струму 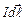в точці простору, що описується вектором (проводиться від елемента струму до даної точки простору); α – кут між елементом струму 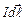та вектором (рис. 4.5).

Напрямок визначається за правилом свердлика: якщо обертати свердлик так, щоб його вістря рухалось за напрямком струму, то ручка свердлика опише лінію магнітної індукції (рис. 4.5). Індукцію поля, створеного в даній точці простору всім провідником, знаходимо за принципом суперпозиції

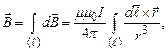(4.11)

Результат інтегрування виразу (4.11) залежить від форми провідника. Зокрема:

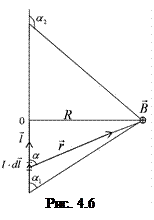
а) розрахуємо магнітне поле прямолінійного струму на відстані R від нього. Як видно з рис. 4.6,

,

,

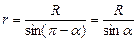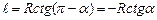звідки

.

Після підстановки двох останніх рівнянь у (4.10) одержимо

.

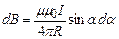Проінтегрувавши останній вираз, отримаємо

;

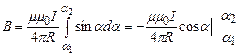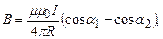
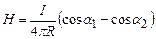; (4.12)

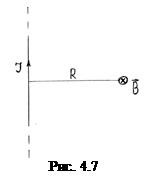
б) вираз для індукції та напруженості магнітного поля нескінченно довгого прямолінійного струму на відстані R від нього (рис. 4.7) одержимо після підстановки в (4.12) ; :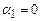

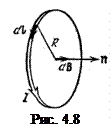
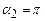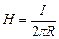, ; (4.13)

в) магнітне поле в центрі колового струму (рис. 4.8)

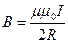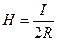, . (4.14)

Дата добавления: 2014-01-04