Циркуляція вектора напруженості магнітного поля. Вихровий характер магнітного поля. Поле довгого соленоїда

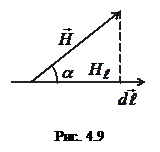Циркуляцією вектора 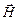по замкненому контуру називається інтеграл 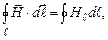де 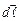- вектор елементу довжини контура, напрямлений вздовж обходу контура, 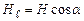– проекція 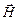на дотичну до контура, α – кут між 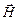та 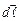(рис. 4.9).

Розглянемо найпростіший випадок – магнітне поле нескінченно довгого прямолінійного струму. Лініями напруженості цього поля є кола, центри яких лежать на осі провідника, а площини перпендикулярні до нього.

Знайдемо циркуляцію 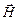вздовж кола радіусом R:

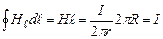, (4.15)

бо .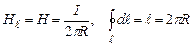

В загальному випадку, коли провідник охоплений замкненою лінією довільної форми (рис. 4.10, а),

,

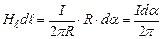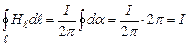. (4.16)

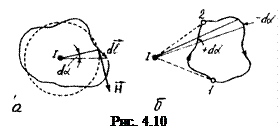Якщо контур не охоплює провідник зі струмом (рис. 4.10, б), то в (4.16) 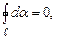адже радіальна пряма спочатку рухається в одному напрямку (ділянка 1-2, 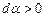), а потім – в іншому (ділянка 2-1, ). Отже,

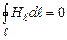. (4.17)

Якщо магнітне поле створюється кількома струмами 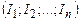, то за принципом суперпозиції 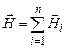і, враховуючи (4.16), остаточно одержимо

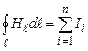. (4.18)

Ця формула є математичним виразом теореми про циркуляцію вектора напруженості магнітного поля: циркуляція вектора напруженості магнітного поля дорівнює алгебраїчній сумі сил струмів, охоплених даним контуром (позитивним вважається струм, що зв’язаний з напрямком обходу правилом свердлика; струм протилежного напрямку вважається негативним). Вираз (4.18) є математичною ознакою вихрового характеру магнітного поля.

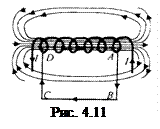
Використаємо теорему про циркуляцію 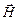для розрахунку магнітного поля довгого соленоїда – циліндричної котушки, на яку намотано N витків дроту. Виберемо контур інтегрування у вигляді прямокутника ABCD, в якому сторона AD лежить всередині соленоїда і паралельна до його осі, а сторона ВС дуже віддалена від соленоїда (рис. 4.11).

Тоді згідно з (4.18)

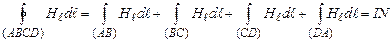. (4.19)

Магнітне поле соленоїда швидко зменшується при віддалені від нього, тому . Крім того, 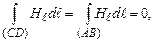оскільки проекція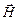на сторони AB і CD дорівнює нулю.

Отже, в лівій частині (4.19) залишається один доданок

.

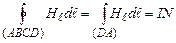Проекція 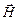на паралельний йому відрізок DA дорівнює модулю цього вектора: , а 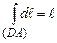(довжина сторони DA).

Таким чином,

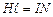і , (4.20)

де 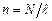– кількість витків на одиниці довжини соленоїда (густина витків). Отже, напруженість магнітного поля всередині довгого соленоїда дорівнює добутку сили струму на густину витків, а індукція поля

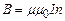. (4.21)

§4.4. Дія магнітного поля на струм; сила Ампера. Магнітна взаємодія струмів

Як відмічалося вище, магнітне поле діє на вміщений у нього провідник зі струмом. Французький фізик Ампер встановив, що на елемент провідника зі струмом 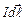, вміщений в магнітне поле індукцією 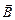, діє сила (сила Ампера)

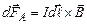(4.22)

або в скалярній формі

, (4.23)

де α – кут між напрямками струму та магнітної індукції. Напрямок сили Ампера можна визначити за правилом лівої руки (рис. 4.12).

Сила, що діє на провідник зі струмом скінченої довжини, знаходиться з (4.22) або (4.23) інтегруванням по всій довжині провідника:

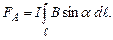(4.24)

Зокрема, для прямолінійного провідника довжиною 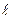в однорідному магнітному полі

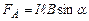. (4.25)

Розглянемо тепер взаємодію двох довгих прямолінійних провідників, паралельних один одному і по яких протікають струми однакового напрямку. Ділянки таких провідників зображені на рис. 4.13.

Сила, з якою магнітне поле першого струму діє на ділянку другого провідника довжиною 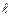, згідно з (4.25)

.

Згідно з (4.13)

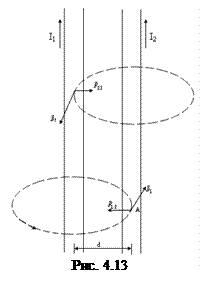
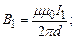
(d – відстань між провідниками).

Як видно з рис. 4.13, кут α між напрямком струму в другому провіднику і вектором магнітної індукції поля першого провідника – прямий; отже, .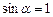

Тоді одержимо

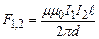. (4.26)

Це і є вираз для сили взаємодії провідників зі струмом (адже так само можна отримати і вираз для сили 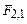). Напрямки сил 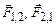знайдені за правилом лівої руки і вказані на рис. 4.13. Отже, струми однакового напрямку притягуються. Аналогічно, можна показати, що антипаралельні струми будуть відштовхуватись.

Із формули (4.26), вважаючи в ній всі величини одиничними (за винятком 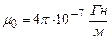), отримаємо визначення одиниці сили струму: ампер – це сила такого постійного струму, який при проходженні по двох прямолінійних паралельних нескінченно довгих провідниках, розміщених на відстані 1 м у вакуумі, викликає між ними магнітну взаємодію силою 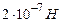на кожен метр довжини. Це визначення використовувалось в СІ до 90-их років минулого століття.

Дата добавления: 2014-01-04