Функции состояния

При изучении изменения свойств системы в процессе используется метод функций. Различают функции состояния и функции перехода (процесса).

Функции состояния – функции независимых параметров, определяющих равновесное состояние термодинамической системы, т.е. это величины, не зависящие от предыстории системы и полностью определяемые ее состоянием в данный момент. Изменение термодинамических функций состояния в процессе перехода от начального состояния (1) до конечного состояния (2) не зависит от пути (характера процесса), а определяется только разностью значений данной функции в конечном и начальном состоянии.

Например, давление газа – однозначная функция объема и температуры. В то же время работа может зависеть от пути перехода системы в конечное состояние, поэтому она является функцией процесса, а не состояния.

Другими словами, если Ф – функция состояния, то

.

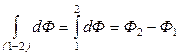Функциями состояния являются внутренняя энергия, энтальпия, энтропия, энергия Гиббса, энергия Гельмгольца и др. Поскольку изменение функции состояния не зависит от пути перехода, то бесконечно малое изменение функции состояния является полным дифференциалом.

Полный дифференциал функции нескольких переменных 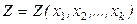равен

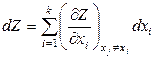. (1.1)

Термодинамические функции чаще рассматриваются как функции двух переменных 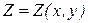и их дифференциал записывается в форме

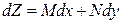(1.2)

При рассмотрении соотношений вида (1.2) самым важным будет установить, является ли полным дифференциал функции Z.

Если dZ – полный дифференциал, то величина изменения функции Z при переходе из состояния (1) в состояние (2) равно разности значений функции Z в этих состояниях:

.

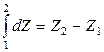Если dZ не является полным дифференциалом, то величина изменения функции Z при переходе из состояния (1) в состояние (2) будет различной в зависимости от того, по какому пути осуществляется переход. Функции, величина изменения которых зависит от пути процесса, называются функциями процесса (теплота, работа).

Далее, если dZ = Mdx + Ndy является полным дифференциалом, то

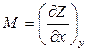и .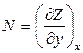

Тогда в соответствии с теоремой Бернули-Эйлера для функции Z = Z (x, y) значение ее второй производной не зависит от порядка дифференцирования

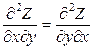. (1.3)

Следовательно,

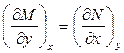. (1.4)

Таким образом, если для дифференциального соотношения типа (1.2) выполняется соотношение (1.4), то дифференциал dZ является полным дифференциалом, а функция Z является функцией состояния.

Если же условие (1.4) не выполняется, то в уравнении (1.2) dZ не является полным дифференциалом, а функция Z будет функцией процесса. Следует иметь в виду, что для дифференциала функции процесса dZ можно найти такую функцию λ (x, y), умножением на которую дифференциал функции процесса dZ превращается в полный дифференциал функции состояния R (x, y):

.

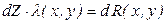Такую функцию λ (х, y) называют интегрирующим множителем. (Например, величина 1/ T является интегрирующим множителем для dQ, где Q – теплота (функция процесса), а dS = dQ / T – полный дифференциал функции состояния энтропии).

Следует отметить также, что Z является функцией состояния, если в круговом (циклическом) процессе ее изменение равно нулю:

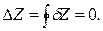
Дата добавления: 2014-01-04