Летучесть (фугитивность) реальных газов

ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА РЕАЛЬНЫХ ГАЗОВ. ЛЕТУЧЕСТЬ

Реальные газы с увеличением давления перестают подчиняться уравнению состояния идеального газа PV = nRT. Более того, при температуре ниже некоторой критической температуры реальные газы при соответствующем повышении давления конденсируются в жидкость и система становится гетерогенной. В настоящее время известно более 150 уравнений состояния таких флюидных систем (флюидные – системы, включающие газообразную и жидкую фазу или одну из них). Наиболее простым из них и качественно правильно передающим поведение реальных газов даже при переходе их в жидкость является уравнение Ван-дер-Ваальса:

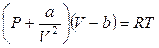, (12.1)

или для n молей газа:

. (12.2)

Это уравнение отличается от уравнения Клапейрона-Менделеева двумя поправками: на собственный объем молекул b и на внутреннее давление а / V ², определяемое взаимным притяжением молекул газа (а и b – константы, не зависящие от Т и Р, но разные для различных газов. Из уравнения (12.2) следует, что

. (12.3)

Для индивидуального идеального газа энергия Гиббса в зависимости от давления при данной температуре вычисляется по формуле

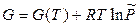. (12.4)

Если газ подчиняется уравнению Ван-дер-Ваальса, то, во-первых,

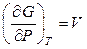, (12.5)

где V – объем, занимаемый реальным газом. Во-вторых, из уравнения (12.3) для 1 моля газа следует, что

,

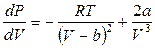. (12.6)

В изотермических процессах

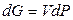, (12.7)

. (12.8)

Интегрирование выражения (12.8) при постоянной температуре приводит к следующему уравнению:

, (12.9)

где G (T) – константа интегрирования (функция только температуры), поскольку

.

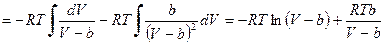Химический потенциал i -го компонента в идеально-газовой смеси равен

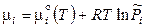. (12.10)

Уравнение состояния смеси 1 моля реальных газов, подчиняющихся уравнению Ван-дер-Ваальса, можно представить следующим образом:

, ,

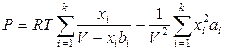, (12.11)

где a_i и b_i – константы уравнения Ван-дер-Ваальса i -го газа; x_i – его мольная доля.

Таким образом, получение в явном виде выражения для энергии Гиббса и химического потенциала реального i -го газа является довольно сложной задачей даже при использовании уравнения Ван-дер-Ваальса. Следовательно, требуется найти общее и достаточно простое ее решение.

Для реального газа можно экспериментально измерить его температуру, давление, объем и рассчитать работу, которую он совершает при изотермическом обратимом изменении (расширении или сжатии) объема

, (12.12)

где P = f (V) – зависимость давления от объема для реального газа.

Для идеального газа работа его изотермического расширения (сжатия) вычисляется по формуле

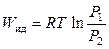, (12.13)

поскольку PV = RT, T = const. Для реального газа, следовательно, можно записать, что

, (12.14)

где f – некоторое свойство реального газа, которое определяет в таком простом соотношении работу изотермического изменения объема реального газа. Это свойство называют летучестью (иногда фугитивностью). Термодинамические соотношения, записанные для идеального газа, становятся справедливыми для реального газа при замене парциального давления на летучесть.

Итак, для реального газа можно записать (Льюис, 1907):

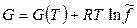, (12.15)

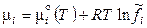. (12.16)

Для количественных расчетов необходимо указать способы определения летучести газа в конкретных условиях.

Из сопоставления выражений (12.13) и (12.14) можно сделать вывод о том, что летучесть – это такое давление, которое должна оказывать идеально-газовая система, чтобы производить такое же действие, что и реальная система. Расчеты показывают, например, что для водорода его летучесть начинает существенно отличаться от давления при давлениях выше 50 атм и при 1000 атм превосходит давление примерно вдвое.

Очевидно, что разность между летучестью и давлением стремится к нулю по мере приближения состояния реального газа к идеальному, то есть при бесконечно малом давлении. Следовательно,

. (12.17)

Для характеристики отклонения свойств реального газа от идеального вводится отношение летучести к давлению, которое называется коэфициентом летучести:

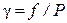, (12.18)

, (12.19)

Следует отметить, что для реальных гетерогенных систем летучесть конденсированной фазы равна летучести насыщенного пара, находящегося в равновесии с этой фазой.

Дата добавления: 2014-01-04