Теплоемкость газов

Теплоемкость газов, жидкостей и кристаллических тел.

Теплоемкость является одной из важнейших характеристик вещества и используется при проведении основных термодинамических расчетов: балансов энергии и энтропии, химических равновесий и др. В связи с этим разрабатываются как экспериментальные, так и теоретические методы определения теплоемкости. В настоящее время существуют точные методы измерения теплоемкости в широком интервале температур. Достигнуты определенные успехи в разработке теории для простого твердого вещества и для его газообразного состояния при невысоких давлениях. Для сложных твердых и жидких веществ пока не существует удовлетворительной теории теплоемкости, поэтому их теплоемкости при отсутствии экспериментальных данных оценивают по приближенным эмпирическим правилам.

Для газов вычисление теплоемкости сводится к определению средней энергии теплового движения отдельных молекул. Для 1 моля идеального газа внутреннюю энергию можно представить в виде суммы:

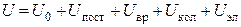, (2.75)

где U ₀ – внутренняя энергия газа при 0 К, в которую включена энергия ядер и электронов при 0 К; U _пост – энергия поступательного движения молекул; U _вр – энергия вращательного движения молекул; U _кол – энергия колебательного движения ядер и групп атомов в молекуле; U _эл – энергия электронов в молекуле.

Последним слагаемым в уравнении (2.75) можно пренебречь, если температура газа не очень высокая, так как для возбуждения электронов требуется значительная энергия. Теплоемкость при Т = 0 К (первое слагаемое) равна нулю. Следовательно, изохорная теплоемкость многоатомного газа С_V будет равна сумме следующих составляющих:

. (2.76)

Согласно классической теории теплоемкости идеальных газов, основанной на законе Больцмана о равном распределении энергии по степеням свободы (закон равнораспределения), на одну степень свободы поступательного и вращательного движения молекулы приходится энергия

(на 1 моль газа ),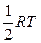

а на степень свободы колебательного движения приходится энергия

kT (на 1 моль газа RT).

На потенциальную энергию гармонических колебаний молекулы приходится такая же тепловая энергия, как и на кинетическую (0,5 kT). В результате на колебательную степень свободы приходится вдвое больше энергии,чем на одну степень свободы поступательного и вращательного движения.

Для одноатомного идеального газа число поступательных степеней свободы равно 3, тогда

С_V = , С_р = С_V + R = , .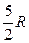

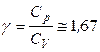Двухатомная молекула помимо 3 поступательных степеней свободы имеет еще 2 вращательные степени свободы. Если атомы в таких молекулах не колеблются (молекула – жесткий ротатор), то число степеней свободы будет равно 5 и

, , .

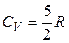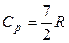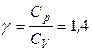Для трехатомных нелинейных молекул (без учета колебательных степеней свободы) число степеней свободы равно6 (3 поступательных и 3 вращательных), тогда

, , .

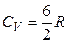Теплоемкость многоатомного идеального газа согласно классической теории теплоемкости с учетом колебательных степеней свободы вычисляется по уравнению:

, (2.77)

где r – число вращательных степеней свободы, s – число колебательных степеней свободы. Число колебательных степеней свободы равно

s = 3 m – 5 для линейных молекул и s = 3 m – 6 для нелинейных молекул,

где m – число атомов в молекуле газа.

Следовательно, максимальная теплоемкость идеального газа С_р по классической теории будет определяться соотношениями:

для линейных молекул:

,

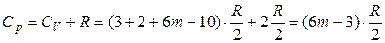; (2.78)

для нелинейных молекул:

,

. (2.79)

Таким образом, согласно классической теории, теплоемкость идеальных газов может принимать значения только кратные 1/2 R, они не должны зависеть от температуры и, при одинаковой атомности и структуре молекул, от природы вещества.

Вычисленные по уравнениям (2.78) и (2.79) теплоемкости газов при обычных температурах соответствуют определенным экспериментально величинам только для одноатомных (инертных) газов. Для двухатомного газа, например, согласно (2.77) С_V =7/2 R, а опытное значение С_V ~ 5/2 R.

Такое расхождение связано с тем, что при вычислении теплоемкости необходимо учитывать квантовые эффекты. Согласно квантовой механике, всякая система частиц, совершающих колебания и вращения, может обладать лишь определенными дискретными значениями энергии. Если энергия теплового движения в системе недостаточна для возбуждения колебаний определенной частоты, то эти колебания не вносят своего вклада в теплоемкость системы. Соответствующая степень свободы оказывается «замороженной» – к ней не применим закон равнораспределения.

Температура, при достижении которой закон равнораспределения оказывается применимым к колебательным степеням свободы, определяется квантово-механическим соотношением

,

где υ – частота колебаний. Величину hυ / k называют характеристической температурой.

Интервалы между вращательными уровнями энергии двухатомной молекулы, деленные на k, составляют всего несколько К и лишь для легких молекул (например, водорода) достигают сотни К. Поэтому вращательные степени свободы при обычных температурах подчиняются закону равнораспределения. Интервалы между колебательными уровнями энергии достигают нескольких тысяч К, поэтому при обычных температурах они «заморожены» и закон равнораспределения не применим к колебательной части теплоемкости. При понижении температуры колебательный вклад в теплоемкость С _кол быстро убывает, стремясь к нулю. Этим объясняется то, что при обычных температурах колебательная часть теплоемкости двухатомного газа практически отсутствует и его молярная изохорная теплоемкость С_V равна 5/2 R вместо 7/2 R.

Экспериментально установлено, что только теплоемкость одноатомных газов слабо зависит от температуры. Теплоемкость же двух- и многоатомных газов заметно увеличивается с ростом температуры. Зависимость теплоемкости газов от температуры можно описать с помощью квантовой теории теплоемкости Эйнштейна.

Если рассматривать каждую колебательную степень свободы как гармонический линейный осциллятор с частотой υ,то ее теплоемкость, согласно Эйнштейну, равна

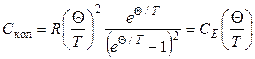, (2.80)

где Θ = hυ / k – характеристическая температура, С_Е (Θ/ T) – функция Планка-Эйнштейна.

В общем случае каждой колебательной степени свободы молекулы соответствует собственная частота колебаний и, следовательно, своя характеристическая температура Θ. Однако в некоторых молекулах может совершаться несколько колебаний с одинаковой частотой. Такие колебания называются вырожденными, а число колебаний с одинаковой частотой – кратностью вырождения. Таким образом, для расчета изохорной теплоемкости газа получаем следующие уравнения:

для линейных молекул:

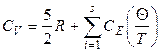; (2.81)

для нелинейных молекул:

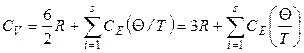. (2.82)

Частоты колебаний молекул находят по инфракрасным спектрам поглощения и спектрам комбинационного рассеяния молекул. В справочниках приводятся данные о частотах колебаний, их вырожденности и характеристических температурах Θ (справочник: табл. 110, стр. 183-188), затем по отношению Θ/ T (аргумента функции Планка-Эйнштейна) по справочникам определяют С_Е – колебательную составляющую теплоемкости, соответствующую данной частоте (справочник: табл. 46, стр. 93-94).

Квантовая теория теплоемкости Эйнштейна позволяет оценивать теплоемкость газов с погрешностью ± 1,5 %, если расчеты ведутся в интервале температур от 293 К и выше.

Дата добавления: 2014-01-04