Теплоемкость кристаллических тел

Согласно правилу Дюлонга и Пти атомная теплоемкость при постоянном объеме для любого твердого вещества приблизительно равна 25 Дж /(моль К) (С_V = 3 R).Это правило выполняется для элементов, атомная масса которых выше, чем у калия, и при относительно высоких температурах.

Теплоемкость химических соединений может быть оценена по эмпирическому правилу Коппа и Неймана, в соответствии с котором молярная теплоемкость соединения в твердом состоянии равна сумме молярных теплоемкостей составляющих его простых веществ:

.

Средняя квадратичная погрешность этого правила составляет ± 7 %.

Простая полуэмпирическая формула, связывающая теплоемкость твердого соединения с температурой первого фазового перехода в конденсированном состоянии T_tr (обычно температура плавления T_fus), предложена Ивановой Л.И:

[Дж/(моль·К)]

где m – число атомов в молекуле соединения.

Правило Дюлонга и Пти, а также стремление теплоемкости к нулю при Т → 0 К, впервые объяснил Эйнштейн (1907 г) на основе квантовой теории теплоемкости. По Эйнштейну, кристалл представляет собой совокупность колеблющихся независимо друг от друга атомов. Причем каждый атом рассматривается как трехмерный гармонический осциллятор. Тогда кристаллическое тело из N атомов образует 3 N гармонических осцилляторов, колеблющихся с одинаковой частотой υ. Энергия линейного гармонического осциллятора определяется уравнением

,

где k – константа Больцмана, h – постоянная Планка. Тогда энергия 1 моля вещества, отнесенная к ее значению при абсолютном нуле, равна

, (2.83)

где N_A – число Авогадро, Θ = hυ / k. Величина Θ имеет размерность температуры и называется характеристической температурой (температурой Эйнштейна Θ _Е).

Поскольку

,

то взяв производную по температуре от (2.83), получим

. (2.84)

Функцию

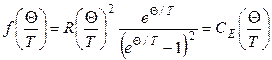(2.85)

называют функцией теплоемкости Эйнштейна-Планка и обозначают C_E (Θ/ T), поэтому уравнение (2.84) можно записать в виде

. (2.86)

Характеристическая температура Θ _Е может быть определена различными методами (по спектрам, по сжимаемости), а также вычислена по приближенным уравнениям. Согласно полуэмпирическому уравнению Линдемана:

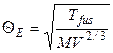, (2.87)

где Т_fus – температура плавления, К; V – молярный объем, м³; M – относительная молекулярная масса.

Анализ формул (2.85) и (2.86) показывает, что, согласно Эйнштейну, при низких температурах (когда kT << hυ, Т << Θ и Θ/ T → ∞) теплоемкость С_V убывает по экспоненциальному закону с понижением температуры и при Т = 0 К теплоемкость С_V должна быть равной нулю. При высоких температурах (когда kT >> hυ, Т >> Θ и Θ/ T → 0) С_V стремится к предельному значению 3 R (правило Дюлонга и Пти).

Однако опыт показывает, что при низких температурах теплоемкость С_V твердых тел изменяется пропорционально Т ³, а не по экспоненциальному закону, как следует из теории Эйнштейна. При низких температурах расхождение между вычисленными теплоемкостями по формуле (2.84) и определенными экспериментально столь значительны (например, вычисленная для меди при 33 К теплоемкость С_V в два с лишним раза меньше ее опытного значения), что квантовую теорию твердого тела Эйнштейна нельзя считать удовлетворительной для этого интервала температур.

Несоответствие теории с экспериментом обусловлено допущением, что атомы кристалла колеблются независимо друг от друга с одинаковой частотой, что недопустимо особенно при низких температурах вследствие малых расстояний между колеблющимися атомами.

Реальный кристалл представляет собой систему связанных осцилляторов с широким частотным спектром колебаний атомов. Поэтому задача нахождения температурной зависимости теплоемкости кристалла связана с определением функции распределения по частотам g (υ), что является трудной экспериментальной задачей. Экспериментально функцию g (υ)определяют методами нейтронографии, теоретически – посредством громоздких численных расчетов.

Простейшей теорией, позволяющей определить функцию распределения частот g (υ) дляодноатомного кристалла, явилась теория теплоемкости Дебая (1912 г). Дебай рассматривал кристалл не как дискретное тело, а как однородную, изотропную, непрерывную среду (упругий континуум), участвующую в колебаниях (продольных и поперечных) с возможными частотами от 0 до υ _max. Максимальное значение частоты υ _maxзависит от природы вещества. Исходя из этих положений, Дебай вывел формулу для теплоемкости твердых веществ

, (2.88)

где ; ; – характеристическая температура (температура Дебая Θ _D).

Значение изохорной теплоемкости

при соответствующих величинах (Θ _D / T) приводятся в таблицах (например, справочник: табл. 48, стр. 96).

Анализируя уравнение (2.88), можно показать, что при Т → ∞ теплоемкость C_V → 3 R, а в области низких температур выполняется соотношение

, (2.89)

где

.

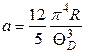Уравнение

называют законом Т-кубов Дебая. В отличие от дебаевского закона, температурный ход теплоемкости ряда веществ в общем случае может быть выражен функцией

,

где n < 3. Так, например, при низких температурах согласно В. В. Тарасову для кристаллов слоистой структуры выполняется соотношение С_V = aT ², а для одномерных или нитевидных структур С_V = aT.

Характеристическая температура Дебая является важнейшим параметром кристалла и зависит от сил, действующих между атомами в кристалле. Чем сильнее силы сцепления, тем выше температура Дебая. Так, например, для свинца Θ _D = 88 K, а для алмаза Θ _D = 1910 К. Температуры Дебая табулированы как физические свойства вещества (справочник: табл. 47, стр. 95).

Температура Дебая дает наиболее удобный в динамической теории кристаллической решетки масштаб температур: величина k Θ _D представляет собой максимальный квант энергии, способный возбудить колебания решетки. При температурах выше температуры Дебая возбуждены все моды, ниже температуры Дебая моды начинают «вымерзать». Температура Дебая отделяет низкотемпературную область, где проявляются квантовые эффекты и где необходимо пользоваться квантовой статистикой, от высокотемпературной, где справедлива классическая статистическая механика.

Величину Θ _D, кроме экспериментальных методов, можно вычислить и по полуэмпирическому уравнению Линдемана:

, (2.90)

где Т_fus – температура плавления, К; V – молярный объем, м³; M – относительная молекулярная масса.

Сравнение уравнений Линдемана для характеристических температур Эйнштейна (2.87) и Дебая (2.90) показывает, что

.

Если по экспериментальным данным по теплоемкости кристалла рассчитать значения температуры Дебая при различных температурах, то обнаруживается, что эта величина заметно изменяется с температурой:

Θ _D = Θ _D (T).

Согласно же модели Дебая характеристическая температура кристалла должна быть постоянной. Зависимость Θ _D от температуры свидетельствует о приближенном характере теории теплоемкости Дебая. Не объясняет теория Дебая и экспериментальный факт линейной зависимости С_V (T) в области высоких температур и оказывается не применимой к сильно анизотропным кристаллам (со сложной структурой).

Объяснить зависимость С_V от Т при высоких температурах удается только при учете ангармонизма колебаний атомов, проявляющегося при больших амплитудах тепловых колебаний. Дискретность структуры кристалла не была учтена, грубым оказалось допущение об изотропности кристалла, в результате чего скорость распространения упругих колебаний в различных направлениях принималась одинаковой.

Следует отметить также, что у металлов определенный вклад в теплоемкость дают и электроны проводимости. Вклад этой электронной составляющей теплоемкости (пропорциональной первой степени температуры) в суммарную теплоемкость металла становится существенным лишь при низких температурах (порядка нескольких К), когда решетчатая теплоемкость С_V становится пренебрежимо малой.

У кристаллических тел с упорядоченным расположением спиновых магнитных моментов атомов (ферро- и антиферромагнетиков) существует дополнительная магнитная составляющая теплоемкости. При температурах фазового перехода в парамагнитное состояние (в точке Кюри или в точке Нееля) эта составляющая теплоемкости испытывает резкий подъем, что является характерной особенностью фазовых переходов второго рода.

Современная теория теплоемкости кристаллов выводит колебательный спектр исходя из структуры и конкретных характеристик межатомных взаимодействий, при этом рассматриваются не только одноатомные, но и молекулярные многоатомные кристаллы. В области высоких температур обязательно учитывается ангармоничность колебаний.

Дата добавления: 2014-01-04