Соотношения Максвелла

Если функции состояния U, H, A, G выразить через их естественные переменные, то они обладают свойством характеристичности и называются термодинамическими потенциалами. Их дифференциалы являются полными, и для простых систем при обратимом протекании процессов равны:

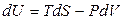, (4.90)

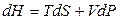, (4.91)

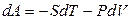, (4.92)

. (4.93)

Используя независимость второй смешенной производной функции двух переменных от порядка дифференцирования, получим:

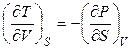, (4.94)

, (4.95)

, (4.96)

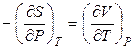. (4.97)

Соотношения (4.94) – (4.97) называются уравнениями Максвелла. Уравнения Максвелла могут быть записаны и в «перевернутом» виде:

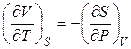и т.д.

Все четыре уравнения Максвелла представляют собой, с одной стороны, производные энтропии или по давлению, или по объему, а с другой стороны, производные объема или давления по температуре. Уравнения Максвелла часто используются в математическом аппарате химической термодинамики.

Так, уравнения (4.96) и (4.97) используют для вычисления энтропии как функции Р и Т или V и Т. Например, для процесса изотермического повышения давления из (4.97) получаем

,

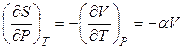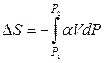. (4.98)

Если принять, что α и V конденсированной фазы не зависят от давления (жидкость или кристалл являются несжимаемым телом), то

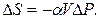(4.99)

Уравнение (4.96) также может быть использовано в теории фазовых равновесий. Для гетерогенного равновесия давление является функцией одной переменной – температуры. Поэтому

.

Значение рассматриваемой производной зависит только от температуры и при Т = const остается постоянной. Поэтому для фазового перехода соотношение (4.96) можно записать в следующем виде:

, ,

а после интегрирования получаем

(4.100)

где Δ_tr H – теплота фазового перехода, Δ_tr V – изменение объема при переходе такого же количества вещества, к которому отнесено Δ_tr H. Уравнение (4.100) и есть знаменитое уравнение Клапейрона-Клаузиуса.

Частные производные химической термодинамики чрезвычайно полезны при решении самых разнообразных задач. При этом следует помнить, что

, .

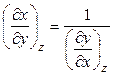Например, требуется найти зависимость изобарной теплоемкости вещества от давления при постоянной температуре. С учетом преобразованного выражения (4.26) и соотношения (4.97)

, ,

получаем

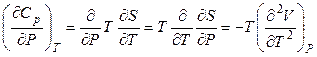(4.101)

Таким образом, если наблюдается близкая к линейной зависимость объема от температуры, то изобарная теплоемкость не изменится. Для количественных расчетов необходимо иметь очень точное уравнение состояния данного вещества.

Другой пример: требуется определить, как изменится температура жидкости в результате ее адиабатического обратимого сжатия. Обратимый адиабатический процесс является изоэнтропийным, поэтому необходимо оценить производную .

Если рассматривать , то

,

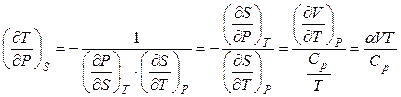. (4.102)

Дата добавления: 2014-01-04