Положительные и отрицательные отклонения от закона Рауля

Реальные растворы.

Реальные растворы подчиняются законам идеальных растворов Pауля и Генри в форме

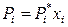
не во всей области концентраций. Если давление насыщенного пара над реальным раствором больше, чем над идеальным раствором того же состава, то отклонения от закона Рауля (отклонения от идеальности) называются положительными, а если меньше – отрицательными. Возможные диаграммы состояния «давление насыщенного пара – состав» для реальных бинарных растворов представлены на рис. 8.6.

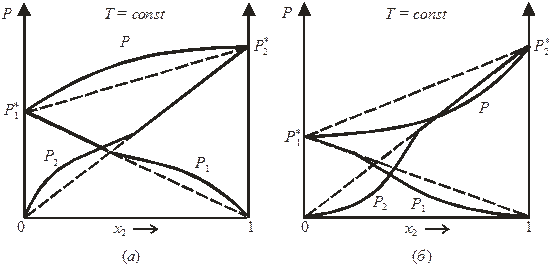
Рис. 8.6. Диаграммы состояния реальных растворов с положительными (а)

и отрицательными (б) отклонениями от идеальности.

Примерами бинарных систем с положительными отклонениями от законов идельных растворов являются растворы (азот – кислород), (ацетон – сероуглерод), (бензол – ацетон), (вода – метиловый спирт); а с отрицательными отклонениями – растворы (вода – азотная кислота), (ацетон – хлороформ), (вода – хлористый водород), (бензол – хлороформ).

Для реальных растворов существуют области концентраций, где выполняются закон Генри для растворенного вещества и закон Рауля для растворителя. Эти области соответствуют предельно (бесконечно) разбавленным растворам. Интервал концентраций, в котором реальные растворы подчиняются правилам бесконечно разбавленных растворов, определяется опытным путем. Например, для растворов неэлектролитов предельная концентрация достигает значений x ₂ = 0,01, а для растворов электролитов значительно меньше – до x ₂ = 10^–6.

Знак и величина отклонения раствора от закона Рауля (от идеальности) зависят от природы растворителя и растворенного вещества и определяются как соотношением размеров молекул обоих компонентов, так и различием в энергиях взаимодействия однородных и разнородных молекул. Дополнительными причинами отклонения могут быть дипольные взаимодействия частиц, образование водородных связей между молекулами, процессы ассоциации и диссоциации.

Идеальные растворы могут быть образованы компонентами, у которых силы взаимодействия между однородными и разнородными молекулами и размеры молекул одинаковы. В этом случае объём раствора равен сумме объёмов растворителя и растворенного вещества и образование раствора не сопровождается выделением или поглощением теплоты. В идеальных растворах свойства отдельных компонентов не отличаются от их свойств в чистом индивидуальном виде.

Свойства реальных растворов зависят от размерного фактора (фактора несоответствия размеров молекул растворителя и растворенного вещества)

,

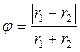где r ₁ и r ₂ – средние радиусы молекул растворителя и растворенного вещества. Чем больше размерный фактор φ, тем больше тенденция раствора к отклонению от закона Рауля.

Если раствор образуется из чистых компонентов 1 и 2, то изменение энергии при образовании раствора (энергия взаимообмена) равно

,

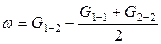где G _1–1 и G _2–2 – энергии взаимодействия между молекулами растворителя и между молекулами растворенного вещества соответственно (энергии взаимодействия однородных молекул), G _1–2 – энергия взаимодействия между молекулами растворителя и растворенного вещества (энергия взаимодействия разнородных молекул). Для идеальных растворов ω = 0, то есть средняя энергия взаимодействия однородных частиц равна энергии взаимодействия разнородных частиц. Если же энергии взаимодействия между однородными и разнородными молекулами значительно различаются, то образование раствора будет сопровождаться изменением объема и выделением или поглощением теплоты.

В тех случаях, когда разнородные молекулы взаимодействуют слабее однородных

, ,

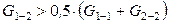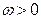смешение компонентов приведет к ослаблению общего межмолекулярного взаимодействия. В результате процесс растворения протекает с увеличением объема и поглощением теплоты. Выход молекул из такого раствора облегчается, давление пара будет выше, чем рассчитанное по закону Рауля – наблюдаются положительные отклонения от законов идеальных растворов. Таким образом, для растворов с положительными отклонениями от закона Рауля, как правило:

, , , .

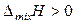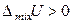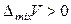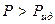Если же разнородные молекулы взаимодействуют сильнее, чем однородные

, ,

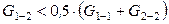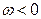то при смешении таких компонентов объем уменьшается и выделяется определенное количество теплоты. Давление пара над таким раствором будет ниже по сравнению с идеальным раствором того же состава – наблюдаются отрицательные отклонения от законов идеальных растворов. Таким образом, для растворов с отрицательными отклонениями от закона Рауля, как правило:

, , , .

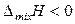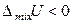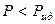При образовании растворов нередко изменяются размеры исходных частиц компонентов за счет разрушения или образования ассоциатов. Если при образовании раствора размеры частиц уменьшаются за счет разрушения ассоциатов, то наблюдаются положительные отклонения от закона Рауля. Если же размеры частиц увеличиваются, то наблюдаются отрицательные отклонения. Следует отметить также, что для реальных систем знак отклонения может изменяться в зависимости от состава раствора. При образовании растворов из элементов выполняется правило Виттига: если образуется раствор из элементов одной подгруппы, то знак отклонения положительный, а если образуется раствор из элементов одного периода, то отрицательный.

Дата добавления: 2014-01-04